题目内容
1.任取$k∈[-\sqrt{3},\sqrt{3}]$,直线y=k(x+2)与圆x2+y2=4相交于A,B两点,则$\left|{\left.{AB}\right|}\right.≥2\sqrt{3}$的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由圆的方程找出圆心坐标和半径r,利用点到直线的距离公式表示出圆心到直线y=k(x+2)的距离d,由r及d,根据垂径定理及勾股定理表示出弦AB的长,令AB的长大于等于2$\sqrt{3}$,列出关于k的不等式,求出不等式的解集得到k的范围,根据已知k的范围,利用几何概型即可求出|AB|≥2$\sqrt{3}$的概率.
解答 解:由圆x2+y2=4,得到圆心为(0,0),半径等于2,
圆心到直线y=k(x+2)的距离d=$\frac{|2k|}{\sqrt{1{+k}^{2}}}$,
由弦长公式得:|AB|=2$\sqrt{4-\frac{{4k}^{2}}{1{+k}^{2}}}$≥2$\sqrt{3}$,
解得:-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$,
又-$\sqrt{3}$≤k≤$\sqrt{3}$,
则|AB|≥2$\sqrt{3}$的概率为$\frac{1}{3}$.
故选:C.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,垂径定理,勾股定理,其他不等式的解法,以及几何概型,当直线与圆相交时,常常根据垂径定理由垂直得中点,然后由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.抛物线的准线方程是$y=\frac{1}{2}$,则其标准方程是( )
| A. | y2=2x | B. | x2=-2y | C. | y2=-x | D. | x2=-y |
6.一个物体的运动方程为s=t2-t+2(其中s的单位是米,t的单位是秒),那么物体在t=4秒的瞬时速度是( )
| A. | 6米/秒 | B. | 7米/秒 | C. | 8米/秒 | D. | 9米/秒 |
13.平面向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(-2,x),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x=( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
10.双曲线$\frac{{x}^{2}}{4}$-y2=1的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
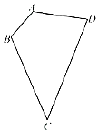 如图所示,已知平面四边形ABCD为凸四边形(凸四边形即任取平面四边形一边所在直线,其余各边均在此直线的同侧),且AB=1,BC=3,CD=4,DA=2,则平面四边形ABCD面积的最大值为$2\sqrt{6}$.
如图所示,已知平面四边形ABCD为凸四边形(凸四边形即任取平面四边形一边所在直线,其余各边均在此直线的同侧),且AB=1,BC=3,CD=4,DA=2,则平面四边形ABCD面积的最大值为$2\sqrt{6}$.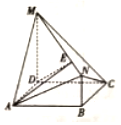 如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.
如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.