题目内容
计算下列定积分
(1)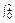 x(x+1)dx;
x(x+1)dx;
(2) (e2x+
(e2x+ )dx;
)dx;
(3) sin2xdx.
sin2xdx.
(1)
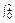 x(x+1)dx;
x(x+1)dx;(2)
 (e2x+
(e2x+ )dx;
)dx;(3)
 sin2xdx.
sin2xdx.(1) (2)
(2) e4-
e4- e2+ln2(3)
e2+ln2(3)
 (2)
(2) e4-
e4- e2+ln2(3)
e2+ln2(3)
(1)∵x(x+1)=x2+x且( x3)′=x2,(
x3)′=x2,( x2)′=x,
x2)′=x,
∴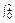 x(x+1)dx=
x(x+1)dx=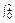 (x2+x)dx
(x2+x)dx
=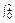 x2dx+
x2dx+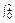 xdx=
xdx= x3|
x3| +
+ x2|
x2| =(
=( ×23-0)+(
×23-0)+( ×22-0)=
×22-0)= .
.
(2)∵(lnx)′= ,(e2x)′=e2x·(2x)′=2e2x,
,(e2x)′=e2x·(2x)′=2e2x,
得e2x=( e2x)′
e2x)′
所以 (e2x+
(e2x+ )dx=
)dx= e2xdx+
e2xdx+
 dx=
dx= e2x|
e2x| +lnx|
+lnx|
= e4-
e4- e2+ln2-ln1=
e2+ln2-ln1= e4-
e4- e2+ln2.
e2+ln2.
(3)由(sin2x)′=cos2x·(2x)′=2cos2x,得
cos2x=( sin2x)′,
sin2x)′,
所以 sin2xdx=
sin2xdx= (
( -
- cos2x)dx
cos2x)dx
=
 dx-
dx-
 cos2xdx
cos2xdx
= x|
x| -
- (
( sin2x)|
sin2x)|
=( -0)-
-0)- (
( sin2
sin2 -
- sin0)=
sin0)= .
.
 x3)′=x2,(
x3)′=x2,( x2)′=x,
x2)′=x,∴
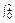 x(x+1)dx=
x(x+1)dx=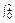 (x2+x)dx
(x2+x)dx=
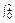 x2dx+
x2dx+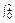 xdx=
xdx= x3|
x3| +
+ x2|
x2| =(
=( ×23-0)+(
×23-0)+( ×22-0)=
×22-0)= .
.(2)∵(lnx)′=
 ,(e2x)′=e2x·(2x)′=2e2x,
,(e2x)′=e2x·(2x)′=2e2x,得e2x=(
 e2x)′
e2x)′所以
 (e2x+
(e2x+ )dx=
)dx= e2xdx+
e2xdx+
 dx=
dx= e2x|
e2x| +lnx|
+lnx|
=
 e4-
e4- e2+ln2-ln1=
e2+ln2-ln1= e4-
e4- e2+ln2.
e2+ln2.(3)由(sin2x)′=cos2x·(2x)′=2cos2x,得
cos2x=(
 sin2x)′,
sin2x)′,所以
 sin2xdx=
sin2xdx= (
( -
- cos2x)dx
cos2x)dx=

 dx-
dx-
 cos2xdx
cos2xdx=
 x|
x| -
- (
( sin2x)|
sin2x)|
=(
 -0)-
-0)- (
( sin2
sin2 -
- sin0)=
sin0)= .
.
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目

 围成的图形的面积.
围成的图形的面积. f(x)dx=-2,求a、b、c的值.
f(x)dx=-2,求a、b、c的值. ,当
,当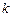 = 时,
= 时,  .恒成立
.恒成立 ,则
,则 =
=