题目内容
已知f（x）=ax2+bx+c，且f（-1）=2，f′（0）=0，
f（x）dx=-2，求a、b、c的值.
f（x）dx=-2，求a、b、c的值.a=6,b=0,c=-4
由f（-1）=2，得a-b+c=2， ①
又f′(x)=2ax+b,
由f′(0)=0得b="0, " ②
f(x)dx=(ax2+bx+c)dx
=(
ax3+
x2+cx)|
=a+
b+c.
即a+b+c=-2， ③
由①②③得：a=6,b=0,c=-4.
又f′(x)=2ax+b,
由f′(0)=0得b="0, " ②
f(x)dx=(ax2+bx+c)dx=(
ax3+x2+cx)|=
a+b+c.即
a+b+c=-2， ③由①②③得：a=6,b=0,c=-4.
练习册系列答案
相关题目
（|x-1|+|x-3|）dx.
，其中G是地球引力常数，M是地球的质量，k是地球的半径.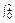
x(x+1)dx;
(e2x+
)dx;
sin2xdx.
与
的图象所围成封闭图形的面积为 .
围成的平面图形的面积．
．