题目内容
6.已知a、b、c分别为△ABC的三个内角A、B、C的对边,若a2+c2=b2+$\sqrt{3}$ac,a=$\sqrt{3}$b,则下列关系可能成立的是①②④.①b=c ②2b=c ③a=c ④a2+b2=c2.
分析 由余弦定理可得cosB=$\frac{\sqrt{3}}{2}$,结合B的范围可求B=$\frac{π}{6}$,又a=$\sqrt{3}$b,利用正弦定理可得sinA=$\frac{\sqrt{3}}{2}$,结合范围A∈(0,π),可得A=$\frac{π}{3}$或$\frac{2π}{3}$,分类讨论利用三角形内角和定理,勾股定理即可得解.
解答 解:∵a2+c2=b2+$\sqrt{3}$ac,
∴a2+c2-b2=$\sqrt{3}$ac,
∴由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{3}ac}{2ac}$=$\frac{\sqrt{3}}{2}$,
∵B∈(0,π),
∴B=$\frac{π}{6}$,
又∵a=$\sqrt{3}$b,
∴利用正弦定理可得:sinA=$\sqrt{3}$sinB=$\frac{\sqrt{3}}{2}$,
∵A∈(0,π),
∴A=$\frac{π}{3}$或$\frac{2π}{3}$,
∴当A=$\frac{π}{3}$时,C=π-A-B=$\frac{π}{2}$,可得:a2+b2=c2,故④正确;
又a=$\sqrt{3}$b,可得:3b2+b2=c2,解得:b=2c,故②正确;
当A=$\frac{2π}{3}$时,C=π-A-B=$\frac{π}{6}$,可得:b=c,此时①正确.
故答案为:①②④.
点评 本题主要考查了余弦定理,正弦定理,三角形内角和定理,勾股定理在解三角形中的应用,考查了计算能力和分类讨论思想,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
16.已知函数y=Asin(ωx+φ)(ω>0,-π≤φ<π)的图象如图所示,则φ的值为(
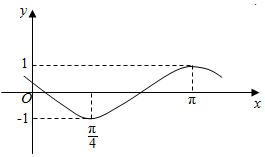

| A. | 0 | B. | -$\frac{5π}{6}$ | C. | $\frac{5π}{6}$ | D. | -$\frac{π}{6}$ |
17.已知a=log43,b=ln3,c=10${\;}^{\frac{1}{2}}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
1.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出S的值为( )


| A. | 3 | B. | 5 | C. | 7 | D. | 10 |
11.设P为双曲线$\frac{x^2}{a^2}$-y2=1(a>0)的上一点,∠F1PF2=$\frac{2π}{3}$,(F1、F2为左、右焦点),则△F1PF2的面积等于( )
| A. | $\sqrt{3}{a^2}$ | B. | $\frac{{\sqrt{3}}}{3}{a^2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
18.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,以点F2为圆心的圆与双曲线的渐近线相切,切点为P.若∠F1PF2=$\frac{2π}{3}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{13}}}{3}$ | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{37}$ |