题目内容
已知a，b，c为互不相等的实数，求证：a4+b4+c4＞abc（a+b+c）
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：运用不等式a2+b2≥2ab（当且仅当a=b取等号），借助累加法和不等式的传递性，即可得证．
解答：
证明：由于a，b，c为互不相等的实数，
则a4+b4＞2a2b2，b4+c4＞2b2c2，c4+a4＞2c2a2，
相加可得，a4+b4+c4＞a2b2+b2c2+c2a2，①
又a2b2+b2c2＞2ab2c，b2c2+c2a2＞2bc2a，c2a2+a2b2＞2ca2b，
相加可得，a2b2+b2c2+c2a2＞ab2c+bc2a+ca2b=abc（a+b+c）．②
由①②可得，a4+b4+c4＞abc（a+b+c）．
则a4+b4＞2a2b2，b4+c4＞2b2c2，c4+a4＞2c2a2，
相加可得，a4+b4+c4＞a2b2+b2c2+c2a2，①
又a2b2+b2c2＞2ab2c，b2c2+c2a2＞2bc2a，c2a2+a2b2＞2ca2b，
相加可得，a2b2+b2c2+c2a2＞ab2c+bc2a+ca2b=abc（a+b+c）．②
由①②可得，a4+b4+c4＞abc（a+b+c）．
点评：本题考查不等式的证明，考查基本不等式的运用，考查累加法证明不等式的方法，考查推理能力，属于中档题．
练习册系列答案
相关题目
下列各项中，不可以组成集合的是（ ）
| A、所以无理数 |
| B、接近于0的数 |
| C、不是质数的数 |
| D、不能被3整除的数 |
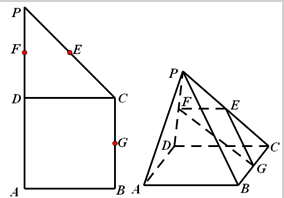在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，DC=2，∠PCD=45°，D，E，F，G分别为线段PA，PC，PD，BC的中点，现将△PDC折起，使平面PDC⊥平面ABCD（图2）．