题目内容
已知点(2,-1)在直线l上的射影为(1,1),则直线l的方程为 .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:由已知得直线l的斜率kl=
,且过(1,1),由此能求出直线l的方程.
| 1 |
| 2 |
解答:
解:∵点(2,-1)在直线l上的射影为(1,1),
k=
=-2,
∴直线l的斜率kl=
,
∴直线l的方程y-1=
(x-1),
整理,得x-2y+1=0.
故答案为:x-2y+1=0.
k=
| 1+1 |
| 1-2 |
∴直线l的斜率kl=
| 1 |
| 2 |
∴直线l的方程y-1=
| 1 |
| 2 |
整理,得x-2y+1=0.
故答案为:x-2y+1=0.
点评:本题考查直线方程的求法,是基础题,解题时要认真审题,注意两直线位置关系的合理运用.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、若命题P为真命题,命题q为假命题,则命题“p∧q”为真命题 | ||
| B、命题“若p则q”的否命题是“若q则p” | ||
| C、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||
D、函数y=
|
sin2014°∈( )
A、(-
| ||||||||
B、(-
| ||||||||
C、(
| ||||||||
D、(
|
下列各项中,不可以组成集合的是( )
| A、所以无理数 |
| B、接近于0的数 |
| C、不是质数的数 |
| D、不能被3整除的数 |
 如图所示,正四棱锥S-ABCD的侧棱长为
如图所示,正四棱锥S-ABCD的侧棱长为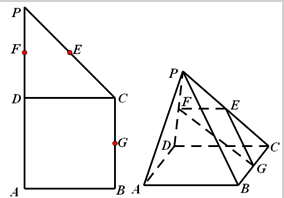 在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,DC=2,∠PCD=45°,D,E,F,G分别为线段PA,PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图2).
在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,DC=2,∠PCD=45°,D,E,F,G分别为线段PA,PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图2).