题目内容
已知向量
=(3,4),向量
满足|
-
|=3,则|
|的取值范围是 .
| a |
| b |
| a |
| b |
| b |
考点:向量的模
专题:平面向量及应用
分析:利用向量模的计算公式、点与圆的位置关系、两点之间的距离公式即可得出.
解答:
解:设
=(x,y),
∴
-
=(3-x,4-y),
∵|
-
|=3,
∴
=3,
化为(x-3)2+(y-4)2=9.圆心C(3,4),半径r=3.
∴|
|=
=5.
∴|
|=
的取值范围是[5-3,5+3],即[2,8].
故答案为:[2,8].
| b |
∴
| a |
| b |
∵|
| a |
| b |
∴
| (3-x)2+(4-y)2 |
化为(x-3)2+(y-4)2=9.圆心C(3,4),半径r=3.
∴|
| OC |
| 32+42 |
∴|
| b |
| x2+y2 |
故答案为:[2,8].
点评:本题考查了向量模的计算公式、点与圆的位置关系、两点之间的距离公式,属于基础题.

练习册系列答案
相关题目
设U={x∈N|-2<x≤3},A={3},则∁UA=( )
| A、{-1,0,1,2,3} |
| B、{1,2,3} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
设集合A={x|x2-5x+6=0},B={x|y=log2(2-x)},则A∩(∁RB)=( )
| A、{2,3} | B、{-1,6} |
| C、{3} | D、{6} |
某程序框图如图,当输入x=3时,则输出的y=( )


| A、1 | B、2 | C、4 | D、8 |
函数f(x)=lg
的定义域为( )
| x2-9 |
| A、[3,+∞) |
| B、(3,+∞) |
| C、(-∞,-3]∪[3,+∞) |
| D、(-∞,-3)∪(3,+∞) |
 如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成.
如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成.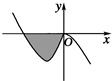 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为