题目内容
已知圆C:(x-a)2+(y-b)2=r2的圆心为抛物线x2=-4y的焦点,直线x+y=1与圆C相切,则该圆的方程为( )
A、(x+1)2+y2=
| ||
| B、x2+(y+1)2=2 | ||
C、(x-2)2+y2=
| ||
D、x2+(y-2)2=
|
考点:抛物线的简单性质
专题:计算题,直线与圆
分析:抛物线x2=-4y的焦点坐标为(1,0),即为圆心坐标,利用圆与直线x+y=1相切,可求半径,即可得到圆的方程.
解答:
解:由题意,抛物线x2=-4y的焦点坐标为(0,-1),即为圆心坐标
∵圆与直线x+y=1相切,∴r=
=
∴圆的方程为x2+(y+1)2=2.
故选:B.
∵圆与直线x+y=1相切,∴r=
| |-1-1| | ||
|
| 2 |
∴圆的方程为x2+(y+1)2=2.
故选:B.
点评:本题考查圆与抛物线的综合,考查直线与圆相切,解题的关键是确定圆的圆心与半径.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
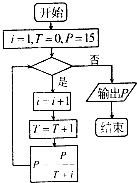 一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的P位于区间(10-4,10-3)内,则判断框内应填入的条件是( )| A、T≤3 | B、T≤4 |
| C、T≤5 | D、T≤6 |
执行如图的程序框图,若输出的S是255,则判断框内应填写( )


| A、n≤6? | B、n≤7? |
| C、n≥7? | D、n≥8? |
已知全集U=R,集合A={x|x<3},B={x|x>2},则图中阴影部分表示的集合为( )


| A、(4,+∞) |
| B、(-∞,3) |
| C、(-∞,2) |
| D、(2,3) |
阅读如图所示程序框图,运行相应程序,则输出的S值为( )


A、-
| ||
B、
| ||
C、
| ||
D、
|
已知圆C:x2+y2=2与直线l:x+y+
=0,则圆C被直线l所截得的弦长为( )
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
二项式(x-
)6的展开式中常数项为( )
| 1 | ||
|
| A、-15 | B、15 |
| C、-20 | D、20 |
某程序框图如图所示,若使输出的结果不大于20,则输入的整数i的最大值为( )


| A、3 | B、4 | C、5 | D、6 |