题目内容
3.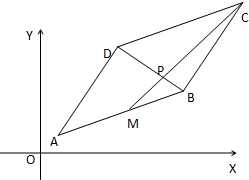 在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.
在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.(1)求直线CM的方程;
(2)求点P的坐标.
分析 (1)由$\overrightarrow{AD}=\overrightarrow{BC}$,可得$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{AD}$=$\overrightarrow{OB}+\overrightarrow{OD}-\overrightarrow{OA}$.利用中点坐标公式可得:点M坐标(4,2).利用斜率计算公式与中点坐标公式即可得出.
(2)利用斜率计算公式可得kBD=-1,利用点斜式可得BD直线方程,联立解出即可得出.
解答 解:(1)∵$\overrightarrow{AD}=\overrightarrow{BC}$,
∴$\overrightarrow{OC}$=$\overrightarrow{OB}$+$\overrightarrow{AD}$=$\overrightarrow{OB}+\overrightarrow{OD}-\overrightarrow{OA}$=(7,3)+(4,6)-(1,1)=(10,8).
∴C点坐标C(10,8).
由中点坐标公式可得:点M坐标($\frac{1+7}{2}$,$\frac{1+3}{2}$),即(4,2).
kCM=$\frac{8-2}{10-4}$=1,
得出直线CM方程y-2=x-4,可得:x-y-2=0.
(2)kBD=$\frac{6-3}{4-7}$=-1,
∴BD直线方程y-6=-(x-4),x+y-10=0,
联立方程组$\left\{\begin{array}{l}{x-y-2=0}\\{x+y-10=0}\end{array}\right.$,
解得x=6,y=4,
所以点P坐标为(6,4).
点评 本题考查了平行四边形的性质、向量的坐标运算性质、点斜式、直线的交点,考查了推理能力与计算能力,属于中档题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{8}$个单位 |
| 气温/℃ | 18 | 13 | 10 | 4 | 0 |
| 杯数 | 24 | 34 | 39 | 51 | 62 |
| A. | y=x+6 | B. | y=-x+42 | C. | y=-2x+60 | D. | y=-3x+78 |
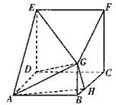 在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.