题目内容
18.在椭圆$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}$=1上有两个动点M,N,K(3,0)为定点,$\overrightarrow{KM}$•$\overrightarrow{KN}$=0,则$\overrightarrow{KM}$•$\overrightarrow{NM}$最小值为9.分析 M在椭圆$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}$=1上,可设M(6cosα,3$\sqrt{3}$sinα)(0≤α<2π),可得$\overrightarrow{KM}$•$\overrightarrow{NM}$=$\overrightarrow{KM}$•$(\overrightarrow{KM}-\overrightarrow{KN})$=${\overrightarrow{KM}}^{2}$-$\overrightarrow{KM}•\overrightarrow{KN}$=(6cosα-3)2+(3$\sqrt{3}$sinα)2
=9(cosα-2)2,利用三角函数的单调性值域与二次函数的单调性即可得出.
解答 解:M在椭圆$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}$=1上,可设M(6cosα,3$\sqrt{3}$sinα)(0≤α<2π),
则$\overrightarrow{KM}$•$\overrightarrow{NM}$=$\overrightarrow{KM}$•$(\overrightarrow{KM}-\overrightarrow{KN})$=${\overrightarrow{KM}}^{2}$-$\overrightarrow{KM}•\overrightarrow{KN}$=${\overrightarrow{KM}}^{2}$=(6cosα-3)2+(3$\sqrt{3}$sinα)2
=36cos2α-36cosα+9+27sin2α=9cos2α-36cosα+36=9(cosα-2)2,
令cosα=t∈[-1,1],则f(t)=9(t-2)2-9∈[9,18].
∴当cosα=1,sinα=0时,即取M(6,0),$\overrightarrow{KM}$•$\overrightarrow{NM}$最小值为9.
故答案为:9.
点评 本题考查了椭圆的定义及其标准方程、向量数量积运算性质、三角函数的单调性值域与二次函数的单调性,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
| A. | [-$\frac{3}{4}$π,$\frac{π}{4}$] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{3}{4}$π] | D. | [-$\frac{π}{2}$,$\frac{π}{2}$] |
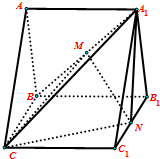 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.M、N分别为A1B、B1C1中点.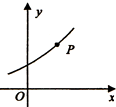 已知函数y=ax+b(b>0)的图象经过点P(1,2),如图所示,则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为3.
已知函数y=ax+b(b>0)的图象经过点P(1,2),如图所示,则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为3.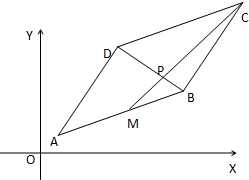 在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.
在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.