题目内容
15.设命题p:|2x-1|≤3;命题q:x2-(2a+1)x+a(a+1)≤0,若¬q是¬p的必要不充分条件,求实数a的取值范围.分析 先分别求出p,q为真时的x的范围,再根据¬q是¬p的必要不充分条件,得到关于a的方程,解得即可.
解答 解:由:|2x-1|≤3得-1≤x≤2,所以¬p是x<-1或x>2,
由x2-(2a+1)x+a(a+1)≤0得:(x-a)[x-(a+1)]≤0,所以a≤x≤a+1,
所以¬q:x<a或x>a+1;
因为¬q是¬p的必要不充分条件,所以$\left\{\begin{array}{l}{a≥-1}\\{a+1≤2}\end{array}\right.$,解得:-1≤a≤1,
所以实数a的取值范围为[-1,1]
点评 本题考查了充分必要条件和不等式的解法,属于基础题.

练习册系列答案
相关题目
7.余弦函数y=cos(x+$\frac{π}{4}$)在下列( )区间为减函数.
| A. | [-$\frac{3}{4}$π,$\frac{π}{4}$] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{3}{4}$π] | D. | [-$\frac{π}{2}$,$\frac{π}{2}$] |
4.在(1+x+$\frac{1}{{x}^{2015}}$)10的展开式中,含x2项的系数为( )
| A. | 10 | B. | 30 | C. | 45 | D. | 120 |
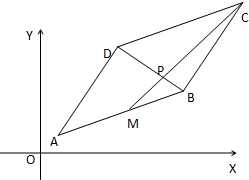 在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.
在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.