题目内容
11.已知函数f(x)=2x3+3ax2-12bx+3在x=-2和x=1处有极值.(1)求出f(x)的解析式;
(2)指出f(x)的单调区间;
(3)求f(x)在[-3,2]上的最大值和最小值.
分析 (1)根据极值的定义得出关于a,b的不等式组,解方程组得出a,b,可得f(x)的解析式;
(2)由f′(x)>0得单调递增区间,f′(x)<0得单调递减区间;
(3)分别求得函数在[-3,2]的极值和端点值,得出最大值及最小值.
解答 解:(1)f'(x)=6x2+6ax-12b,
又因为函数y=f(x)在x=-2和x=1处有极值,
所以 $\left\{\begin{array}{l}{f′(-2)=0}\\{f′(1)=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$,
所以f(x)=2x3+3x2-12x+3;
(2)f'(x)=6(x+2)(x-1)
由f'(x)>0,得x<-2或x>1,f'(x)<0,得-2<x<1
所以f(x)的单调递增区间为(-∞,-2),(1,+∞),递减区间为(-2,1);
(3)令f'(x)=0,得x=-2或x=1,f(-2)=23,f(1)=-4,f(-3)=12,f(2)=7,
所以f(x)的最大值为f(-2)=23,最小值为f(1)=-4.
点评 本题考查函数导数与单调性,考查学生运用所学知识分析解决问题的能力,属中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
16.已知集合A={y|y=x${\;}^{\frac{2}{3}}$,x≥1},B={y|y=($\frac{1}{2}$)x,x≥-1},则A∩B=( )
| A. | {y|1≤y≤2} | B. | {y|y≥2} | C. | {y|$\frac{1}{2}$≤y≤1} | D. | {y|y≥1} |
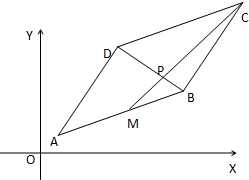 在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.
在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P.