题目内容

1．在等比数列{an}中，若a1+a2=5，a3+a4=15，则a5+a6的值为（　　）
A．25B．20C．75D．45

分析 由已知，结合（a1+a2），（a3+a4），（a5+a6）成等比数列得答案．

解答 解：在等比数列{an}中，由a1+a2=5，a3+a4=15，得
$（{a}_{3}+{a}_{4}）^{2}=（{a}_{1}+{a}_{2}）（{a}_{5}+{a}_{6}）$，
∴${a}_{5}+{a}_{6}=\frac{（{a}_{3}+{a}_{4}）^{2}}{{a}_{1}+{a}_{2}}=\frac{1{5}^{2}}{5}=45$．
故选：D．

点评 本题考查等比数列的通项公式，考查了等比数列的性质，是基础题．

练习册系列答案
相关题目
11．在△ABC中，a=5，b=4，C=60°，则$\overrightarrow{CB}$•$\overrightarrow{CA}$的值为（　　）
A．-10B．10C．-10$\sqrt{3}$D．10$\sqrt{3}$
12．设x，y∈R，则“x，y≥1”是“x2+y2≥2”的（　　）
A．既不充分也不必要条件B．必要不充分条件
C．充要条件D．充分不必要条件
9．在△ABC中，A、B、C的对边分别为a，b，c，已知A≠$\frac{π}{2}$，且3sinAcosB+$\frac{1}{2}$bsin2A=3sinC．
（I）求a的值；
（Ⅱ）若A=$\frac{2π}{3}$，求△ABC周长的最大值．
16．已知函数f（x）=（$\frac{1}{2}$）x-1和g（x）=-10x+20，则二者图象的交点的横坐标所属区间为（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
6．已知a，b，c分别是△ABC内角A，B，C，的对边，若asinC=2sinA．
（1）求c的值；
（2）若a=$\sqrt{3}$，b=3，求△ABC的面积．
13．某几何体的三视图如图所示（单位：cm），则该几何体的表面积等于（　　）
A．8πcm2B．7πcm2C．6πcm2D．5πcm2
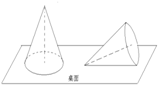9．用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥，放在水平桌面上，被一阵风吹倒，如图，则它的最高点到桌面的距离为5$\sqrt{3}$cm．
10．双曲线x2-4y2=-1的渐进线方程为x±2y=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网