题目内容
定义函数y=f(x),x∈D(D为定义域)图象上的点到坐标原点的距离为函数的y=f(x),x∈D的模.若模存在最大值,则此最大值称之为函数y=f(x),x∈D的长距;若模存在最小值,则此最小值称之为函数y=f(x),x∈D的短距.
(1)分别判断函数f1(x)=
与f2(x)=
是否存在长距与短距,若存在,请求出;
(2)对于任意x∈[1,2]是否存在实数a,使得函数f(x)=
的短距不小于2,若存在,请求出a的取值范围;不存在,则说明理由?
(1)分别判断函数f1(x)=
| 1 |
| x |
| -x2-4x+5 |
(2)对于任意x∈[1,2]是否存在实数a,使得函数f(x)=
| 2x|x-a| |
考点:进行简单的合情推理
专题:计算题,函数的性质及应用
分析:(1)可以由基本不等式及长距和短距的定义求出;
(2)将a进行分类讨论通过解不等式求出a的范围即可.
(2)将a进行分类讨论通过解不等式求出a的范围即可.
解答:
解:(1)设u(x)=
≥
(当且仅当x=±1取得等号),f1(x)短距为
,长距不存在.
设v(x)=
=
,x∈[-5,1],
v(x)min=v(1)=1v(x)max=v(-5)=5,
f2(x)短距为1,长距为5.
(2)设h(x)=
,x∈[1,2],
函数f(x)=
的短距不小于2,即x2+2x|x-a|≥4对于x∈[1,2]始终成立:
当a>2时:a≥
(x+
)对于x∈[1,2]始终成立,
∴a≥
,
当1≤a≤2时:取x=a即可知显然不成立
当a<1时:a≤
(3x-
)对于x∈[1,2]始终成立
∴a≤-
综上所述:存在实数a∈(-∞,-
]∪[
,+∞),使得函数f(x)=
的短距不小于2.
x2+
|
| 2 |
| 2 |
设v(x)=
| x2+(-x2-4x+5) |
| 5-4x |
v(x)min=v(1)=1v(x)max=v(-5)=5,
f2(x)短距为1,长距为5.
(2)设h(x)=
| x2+2x|x-a| |
函数f(x)=
| 2x|x-a| |
当a>2时:a≥
| 1 |
| 2 |
| 4 |
| x |
∴a≥
| 5 |
| 2 |
当1≤a≤2时:取x=a即可知显然不成立
当a<1时:a≤
| 1 |
| 2 |
| 4 |
| x |
∴a≤-
| 1 |
| 2 |
综上所述:存在实数a∈(-∞,-
| 1 |
| 2 |
| 5 |
| 2 |
| 2x|x-a| |
点评:本题新定义了长距和短距,属于新定义问题,用到了基本不等式及函数的最值问题,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
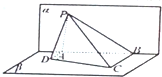 如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )
如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )| A、椭圆的一部分 |
| B、线段 |
| C、双曲线的一部分 |
| D、以上都不是 |
k>5是方程
+
=1的曲线为椭圆时的( )
| x2 |
| k-5 |
| y2 |
| 6-k |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、非充分非必要条件 |