题目内容
10.已知函数y=$\frac{f(x)}{{e}^{x}}$是偶函数且在[0,+∞)上单调递增,则下列说法中正确的是( )| A. | ef(1)<f(2) | B. | e3f(-1)>f(2) | C. | e2f(-1)<f(1) | D. | ef(-2)<f(-1) |
分析 由题意函数y=$\frac{f(x)}{{e}^{x}}$是偶函数且在[0,+∞)上单调递增,可得$\frac{f(2)}{{e}^{2}}$>$\frac{f(1)}{e}$,即可得出结论.
解答 解:由题意函数y=$\frac{f(x)}{{e}^{x}}$是偶函数且在[0,+∞)上单调递增,
∴$\frac{f(2)}{{e}^{2}}$>$\frac{f(1)}{e}$,
∴ef(1)<f(2),
故选A.
点评 本题考查函数单调性的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
18.实部为1,虚部为2的复数所对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.sin300°+cos390°+tan(-135°)=( )
| A. | $\sqrt{3}$-1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
2.过点M(-2,0)的直线l与椭圆x2+2y2=4交于P1,P2两点,设线段P1P2的中点为P.若直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
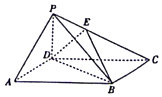 如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底要ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.