题目内容
2.过点M(-2,0)的直线l与椭圆x2+2y2=4交于P1,P2两点,设线段P1P2的中点为P.若直线l的斜率为k1(k1≠0),直线OP的斜率为k2,则k1k2等于( )| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 设直线l的方程为y=k1(x+2),代入x2+2y2=2,得(1+2k12)x2+8k12x+8k12-2=0,然后由根与系数的关系求解能够得到k1k2的值.
解答 解:设P1(x1,y1),P2(x2,y2),中点P(x0,y0),
设直线l的方程为y=k1(x+2),代入x2+2y2=2,得(1+2k12)x2+8k12x+8k12-2=0,
所以x1+x2=-$\frac{8{{k}_{1}}^{2}}{1+2{{k}_{1}}^{2}}$.而y1+y2=k1(x1+x2+4)=$\frac{4{k}_{1}}{1+2{{k}_{1}}^{2}}$.
所以OP的斜率k2=$\frac{{y}_{0}}{{x}_{0}}=\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{1}{2{k}_{1}}$
所以k1k2=-$\frac{1}{2}$
故选:D
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答.属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
13.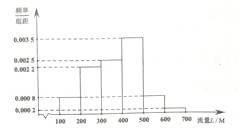 某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
(1)从该校教师中随机抽取3人,求这3人中至多有1人月使用流量不超过300M的概率;
(2)现该通讯商推出三款流量套餐,详情如下:
这三款套餐都有如下附加条款:套餐费月初一次性收取,手机使用一旦超出套餐流量,系统就自动帮用户充值200M流量,资费20元;如果又超出充值流量,系统就再次自动帮用户充值200M流量,资费20元/次,依此类推,如果当流量有剩余,系统将自动清零,无法转入次月使用.
学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的75%,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.
 某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.
某学校为鼓励家校互动,与某手机通讯商合作,为教师伴侣流量套餐,为了解该校教师手机流量使用情况,通过抽样,得到100位教师近2年每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如下:若将每位教师的手机月平均使用流量分布视为其手机月使用流量,并将频率为概率,回答以下问题.(1)从该校教师中随机抽取3人,求这3人中至多有1人月使用流量不超过300M的概率;
(2)现该通讯商推出三款流量套餐,详情如下:
| 套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
| A | 20 | 300 |
| B | 30 | 500 |
| C | 38 | 700 |
学校欲订购其中一款流量套餐,为教师支付月套餐费,并承担系统自动充值的流量资费的75%,其余部分由教师个人承担,问学校订购哪一款套餐最经济?说明理由.
10.已知函数y=$\frac{f(x)}{{e}^{x}}$是偶函数且在[0,+∞)上单调递增,则下列说法中正确的是( )
| A. | ef(1)<f(2) | B. | e3f(-1)>f(2) | C. | e2f(-1)<f(1) | D. | ef(-2)<f(-1) |
7.在等差数列{an}中,a1=-2012,其前n项和为Sn,若$\frac{{S}_{2012}}{2012}$-$\frac{{S}_{10}}{10}$=2002,则S2017=( )
| A. | 8068 | B. | 2017 | C. | -8027 | D. | -2013 |
11.若函数f(x)在R上可导,且f(x)=x2+2f′(1)x+3,则( )
| A. | f(0)<f(4) | B. | f(0)=f(4) | C. | f(0)>f(4) | D. | 无法确定 |
12.方程x2+y2cosα=1(α∈R)不能表示的曲线为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |