题目内容
19.已知等差数列{an}的前n项和Sn,且a3=7,S11=143,(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2${\;}^{{a}_{n}}$+2n,求数列{bn}的前n项和Tn.
分析 (Ⅰ)由等差数列的通项公式和前n项和公式求得该数列的首项和公差即可;
(Ⅱ)结合(Ⅰ)的通项公式求得数列{bn}的通项公式,然后利用分组求和法求Tn.
解答 解:(Ⅰ)由a3=7,S11=143,得
$\left\{\begin{array}{l}{{a}_{1}+2d=7}\\{11{a}_{1}+\frac{11×(11-1)}{2}d=143}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=3}\\{d=2}\end{array}\right.$,
所以an=2n+1;
(Ⅱ)因为an=2n+1,
所以bn=2${\;}^{{a}_{n}}$+2n=2×4n+2n,
所以Tn=b1+b2+b3+…+bn=2(4+42+43+…+4n)+2(1+2+3+…+n)
=$\frac{8}{3}$×4n+n2+n-$\frac{8}{3}$.
点评 本题主要考查数列通项公式和前n项和的求解,利用分组求和法是解决本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
10.已知函数y=$\frac{f(x)}{{e}^{x}}$是偶函数且在[0,+∞)上单调递增,则下列说法中正确的是( )
| A. | ef(1)<f(2) | B. | e3f(-1)>f(2) | C. | e2f(-1)<f(1) | D. | ef(-2)<f(-1) |
7.在等差数列{an}中,a1=-2012,其前n项和为Sn,若$\frac{{S}_{2012}}{2012}$-$\frac{{S}_{10}}{10}$=2002,则S2017=( )
| A. | 8068 | B. | 2017 | C. | -8027 | D. | -2013 |
4.设等差数列{an}满足sina4cosa7-cosa4sina7=1,公差d∈(-1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
| A. | $(\frac{7π}{6},\frac{4π}{3})$ | B. | $[{\frac{7π}{6},\frac{4π}{3}}]$ | C. | $(\frac{4π}{3},\frac{3π}{2})$ | D. | $[{\frac{4π}{3},\frac{3π}{2}}]$ |
11.若函数f(x)在R上可导,且f(x)=x2+2f′(1)x+3,则( )
| A. | f(0)<f(4) | B. | f(0)=f(4) | C. | f(0)>f(4) | D. | 无法确定 |
8.已知△ABC的内角A,B,C的对边分别是a,b,c,若cos C=$\frac{\sqrt{5}}{5}$,b=atan C,则$\frac{sinB}{sinA}$等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
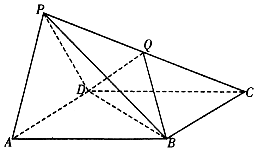 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.