题目内容
已知命题p:指数函数f(x)=(2a-6)x在R上单调递减,命题q:关于x的方程x2-3ax+2a2+1=0的两个实根均大于3.若p或q为真,p且q为假,求实数a的取值范围.
{a|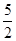 <a≤3或a≥
<a≤3或a≥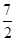 }.
}.
解析试题分析:若p真,则f(x)=(2a-6)x在R上单调递减,
∴0<2a-6<1,∴3<a<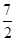 ,
,
若q真,令f(x)=x2-3ax+2a2+1,则应满足 ,
,
∴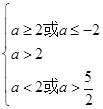 ,故a>
,故a>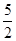 ,
,
又由题意应有p真q假或p假q真. 6分
①若p真q假,则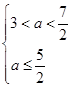 ,a无解.
,a无解.
②若p假q真,则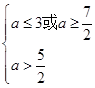 ,
,
∴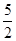 <a≤3或a≥
<a≤3或a≥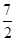 . 6分
. 6分
故a的取值范围是{a|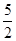 <a≤3或a≥
<a≤3或a≥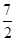 }. 14分
}. 14分
考点:指数函数的单调性;二次方程根的分布问题;复合命题真假的判断。
点评:⑴本题主要考查一个一元二次方程根的分布问题.在二次项系数不确定的情况下,一定要分二次项系数分为0和不为0两种情况讨论.
⑵设一元二次方程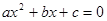 (
(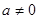 )的两个实根为
)的两个实根为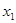 ,
,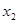 ,且
,且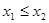 。
。
① 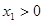 ,
,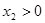 (两个正根)
(两个正根)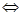
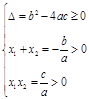 ;
;
② 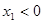 ,
,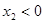 (两个负根)
(两个负根)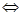
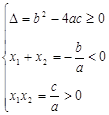 ;
;
③ 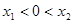 (一个正根一个负根)
(一个正根一个负根)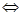
 。
。

练习册系列答案
相关题目
 令
令 .
. 的表达式;
的表达式; 和函数
和函数 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围. .
.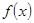 在
在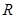 上为增函数;
上为增函数; 的值;
的值; 上的值域.
上的值域.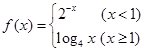 ,
,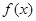 的图像;
的图像;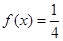 的
的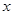 的取值.
的取值.
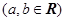 .
. 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是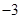 ,求
,求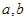 的值;
的值;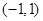 上不单调,求
上不单调,求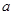 的取值范围.
的取值范围.
 的定义域;
的定义域; ,求
,求 的值.
的值.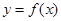 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数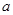 使得
使得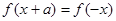 成立,则称此函数具有“
成立,则称此函数具有“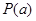 性质”.
性质”.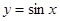 是否具有“
是否具有“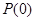 性质”,且当
性质”,且当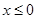 时
时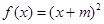 ,求
,求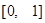 上的最大值.
上的最大值.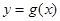 具有“
具有“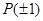 性质”,且当
性质”,且当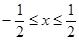 时,
时,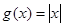 .若
.若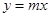 交点个数为2013个,求
交点个数为2013个,求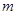 的值.
的值.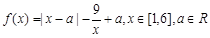 。
。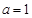 ,试判断并证明
,试判断并证明 的单调性;
的单调性;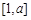 上单调,且存在
上单调,且存在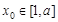 使
使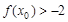 成立,求
成立,求 的取值范围;
的取值范围;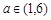 时,求函数
时,求函数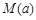 。
。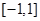 上的奇函数
上的奇函数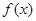 ,当
,当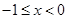 时,
时,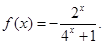
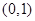 上的单调性,并给予证明;
上的单调性,并给予证明;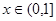 时,关于
时,关于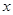 的方程
的方程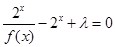 有解,试求实数
有解,试求实数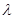 的取值范围.
的取值范围.