题目内容
(本题12分)已知函数
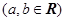 .
.
⑴若函数 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是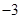 ,求
,求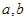 的值;
的值;
⑵若函数 在区间
在区间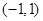 上不单调,求
上不单调,求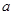 的取值范围.
的取值范围.
⑴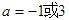 ,
,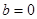 . ⑵
. ⑵ .
.
解析试题分析:⑴已知函数 的图象过原点,则
的图象过原点,则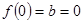 .
. ,已知函数
,已知函数 的图象在原点处的切线斜率是
的图象在原点处的切线斜率是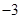 ,则
,则 ,
,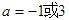 .
.
所以,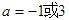 ,
,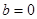 . ………………………………………………6分.
. ………………………………………………6分.
⑵
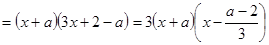 ,求得方程
,求得方程 的两个实根:
的两个实根: . ………………………………9分.
. ………………………………9分.
函数 在区间
在区间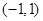 上不单调
上不单调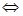
 在区间
在区间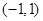 上至少存在一个极值点
上至少存在一个极值点
 或
或 ,即
,即 或
或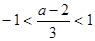 ,解之(合并)得
,解之(合并)得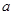 的取值范围:
的取值范围: . ………………………………12分.
. ………………………………12分.
考点:本题主要考查导数的应用—研究单调性、极值,导数的几何意义。
点评:中档题,曲线上某点切线的斜率,等于该点的导函数值。

练习册系列答案
相关题目
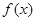 满足
满足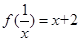 .
.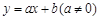 ,
,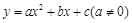 ,
,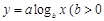 且
且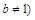 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.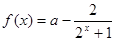 ,其中
,其中 为常数
为常数 为奇函数,试确定
为奇函数,试确定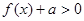 恒成立,求实数
恒成立,求实数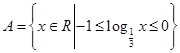 ,函数
,函数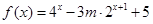 (其中
(其中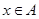 ,
, )
)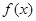 的定义域;
的定义域;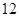 分)已知函数
分)已知函数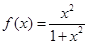 .
.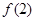 与
与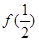 ,
,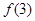 与
与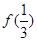 ;
; 与
与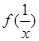 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;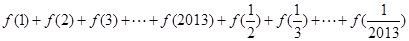 的值 .
的值 .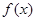 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,求:
,求: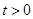 ,求函数
,求函数 上的最小值。
上的最小值。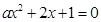 至少有一个负实根的充要条件。
至少有一个负实根的充要条件。