题目内容
(本小题满分12分)
已知 令
令 .
.
(1)求 的表达式;
的表达式;
(2)若函数 和函数
和函数 的图象关于原点对称,
的图象关于原点对称,
(ⅰ)求函数 的解析式;
的解析式;
(ⅱ)若 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
(1) = -sin2x+2sinx (2)
= -sin2x+2sinx (2)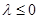
解析试题分析:
解:(1) 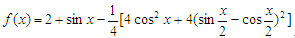

(2)设函数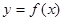 的图象上任一点
的图象上任一点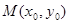 关于原点的对称点为
关于原点的对称点为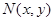
则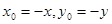 ,∵点
,∵点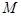 在函数
在函数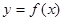 的图象上
的图象上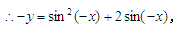
即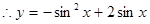
∴函数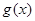 的解析式为
的解析式为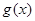 = -sin2x+2sinx
= -sin2x+2sinx
(Ⅲ)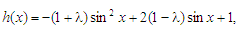
设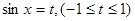
则有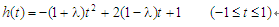
当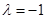 时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
当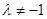 时,对称轴方程为直线
时,对称轴方程为直线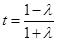 .
.
ⅰ) 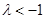 时,
时,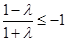 ,解得
,解得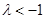
ⅱ)当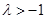 时,
时,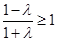 ,解得
,解得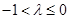
综上,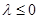 .
.
考点:本试题考查了三角函数的性质。
点评:对于三角函数的性质的研究,一般首先是将函数化为单一函数,同时能利用三角函数的性质分析得到其结论。而对于函数给定区间的递增性质,结合了二次函数,因此对于对称轴和定义域的关系加以讨论得到,属于难度试题。

练习册系列答案
相关题目
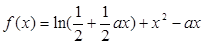
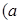 为常数,
为常数,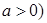
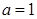 时,求函数
时,求函数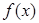 在
在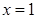 处的切线方程;
处的切线方程; 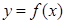 在
在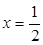 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程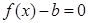 在
在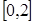 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数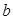 的取值范围;
的取值范围;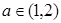 ,总存在
,总存在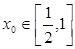 ,使不等式
,使不等式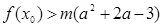 成立,求实数
成立,求实数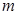 的取值范围。
的取值范围。 求
求
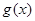 分别由下表给出:
分别由下表给出:
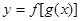 ,并画出函数
,并画出函数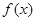 满足
满足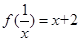 .
. ,其中
,其中 ,且a≠0.
,且a≠0. 在区间[1,e]上的最小值;
在区间[1,e]上的最小值; ,
, ,其中
,其中 .
. ,求
,求 的值;
的值; ,求
,求