题目内容
定义在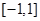 上的奇函数
上的奇函数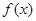 ,当
,当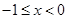 时,
时,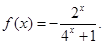
(1)求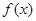 在
在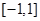 上的解析式;
上的解析式;
(2)判断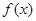 在
在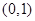 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当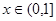 时,关于
时,关于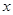 的方程
的方程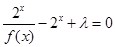 有解,试求实数
有解,试求实数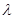 的取值范围.
的取值范围.
(1)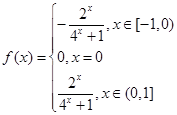 (2)
(2)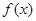 在
在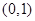 上为减函数,证明见解析(3)
上为减函数,证明见解析(3)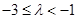
解析试题分析:(1)∵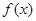 在
在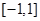 上是奇函数,∴
上是奇函数,∴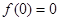 , ……1分
, ……1分
设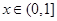 ,则
,则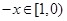 ,
,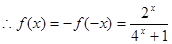 , ……3分
, ……3分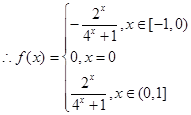 . ……4分
. ……4分
(2)设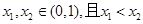 ,则
,则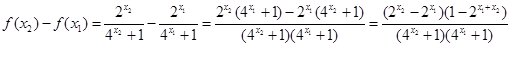 , ……6分
, ……6分
∵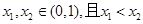 ,∴
,∴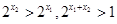 ,
,
又 ,
, ,
,
所以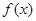 在
在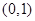 上为减函数. ……8分
上为减函数. ……8分
(3)当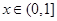 时,
时,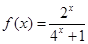 ,则方程
,则方程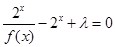 化为
化为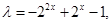 ……10分
……10分
∵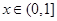 ,
,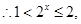
而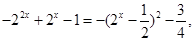
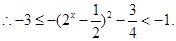 ……11分
……11分
因此要使方程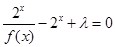 有解,只须
有解,只须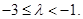 ……12分
……12分
考点:本小题主要考查利用函数的奇偶性求分段函数的表达式、利用定义证明函数的单调性和复合函数的值域问题,考查学生分析问题、解决问题的能力和转化问题的能力以及运算求解能力.
点评:奇函数如果在原点处有定义,则一定有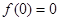 ;用定义域证明函数的单调性性时,一定要把结果化到最简,而第三问将问题转化为复合函数的值域问题是解决第三问的关键.
;用定义域证明函数的单调性性时,一定要把结果化到最简,而第三问将问题转化为复合函数的值域问题是解决第三问的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
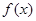 是定义在
是定义在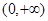 上的增函数,且对一切
上的增函数,且对一切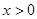 满足
满足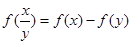 .
.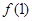 的值;
的值;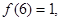 解不等式
解不等式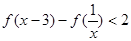 .
. 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足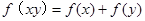 ,
, 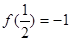
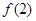 =1 (2) 求不等式
=1 (2) 求不等式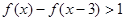 的解集.
的解集. 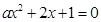 至少有一个负实根的充要条件。
至少有一个负实根的充要条件。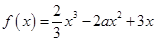 (
(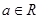 ).
).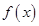 的单调区间;
的单调区间;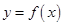 在
在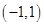 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.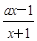 ,其中a∈R.
,其中a∈R.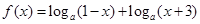 ,
,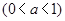
 的定义域;
的定义域;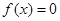 ,求
,求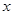 的值;
的值;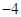 ,求
,求 的值.
的值.