题目内容
(本小题满分8分)已知函数 .
.
(1)求证:函数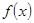 在
在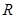 上为增函数;
上为增函数;
(2)当函数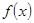 为奇函数时,求
为奇函数时,求 的值;
的值;
(3)当函数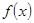 为奇函数时, 求函数
为奇函数时, 求函数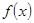 在
在 上的值域.
上的值域.
(1)任取 则
则

 因为
因为 所以
所以 ,
, ,
, 故
故 ,所以
,所以 在R上为增函数
在R上为增函数
(2) (3)
(3)
解析试题分析:(1)任取 则
则

 因为
因为 所以
所以 ,
, ,
, 故
故
所以 在R上为增函数………………3分
在R上为增函数………………3分
(2)因 在x=0 有意义,又
在x=0 有意义,又 为奇函数,则
为奇函数,则
即 ……………………5分
……………………5分
(3)由x∈[-1,2]得 
 ……… ……8分
……… ……8分
考点:本题考查了函数的性质及值域的求法
点评:掌握函数单调性的步骤及应用时解决函数问题的常见方法

练习册系列答案
相关题目
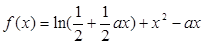
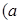 为常数,
为常数,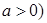
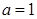 时,求函数
时,求函数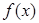 在
在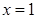 处的切线方程;
处的切线方程; 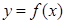 在
在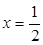 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程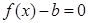 在
在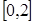 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数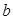 的取值范围;
的取值范围;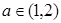 ,总存在
,总存在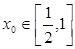 ,使不等式
,使不等式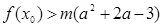 成立,求实数
成立,求实数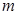 的取值范围。
的取值范围。 ,
, ,其中
,其中 .
. ,求
,求 的值;
的值; ,求
,求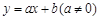 ,
,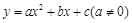 ,
,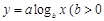 且
且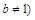 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量. 的偶函数
的偶函数 .
.  的值;
的值;  的单调性;
的单调性; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 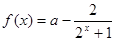 ,其中
,其中 为常数
为常数 为奇函数,试确定
为奇函数,试确定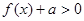 恒成立,求实数
恒成立,求实数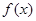 是定义在
是定义在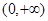 上的增函数,且对一切
上的增函数,且对一切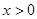 满足
满足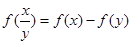 .
.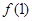 的值;
的值;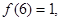 解不等式
解不等式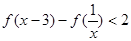 .
.