题目内容
已知函数
(1)求函数 的定义域;
的定义域;
(2)求函数 的零点;
的零点;
(3)若函数 的最小值为
的最小值为 ,求
,求 的值.
的值.
(1)  (2)零点是
(2)零点是 (3)
(3)
解析试题分析:解:(1)要使函数有意义:则有 ,
,
解之得: ,
,
所以函数的定义域为: 3分
3分
(2)函数可化为
由 ,得
,得 ,
,
即 ,
, 5分
5分 ,
, 的零点是
的零点是 7分
7分
(3)函数可化为:

∵ ∴
∴ 9分
9分 ,
, ,即
,即 11分
11分
由 ,得
,得 ,
, 12分
12分
考点:本试题主要是考查了对数函数的定义域的求解,以及函数零点的概念,以及函数最值问题的应用是中档试题。
点评:解决函数的性质问题,首要的是求解函数的定义域,然后分析表达式,变形化简,进而求解函数的零点,通过解方程得到。结合单调性得到最值,这是最值的一般思路。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中
,其中 ,且a≠0.
,且a≠0. 在区间[1,e]上的最小值;
在区间[1,e]上的最小值; 的偶函数
的偶函数 .
.  的值;
的值;  的单调性;
的单调性; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  .
. 的单调性;
的单调性; 的值;
的值; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
,
 时,求函数
时,求函数 的极值;
的极值; 的取值范围.
的取值范围.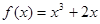 ,若
,若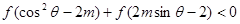 对
对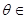 R
R 的取值范围.
的取值范围. 和
和 是函数
是函数 的两个极
的两个极 ,
, .(Ⅰ) 求
.(Ⅰ) 求 的取值范围;
的取值范围; ,求
,求 的最大值.
的最大值.