题目内容
17．已知$\frac{1}{2}$＜a＜4，函数f（x）=x3-3bx2+a有且仅有两个不同的零点x1，x2，则|x1-x2|的取值范围是（ ）| A． | （$\frac{1}{2}$，1） | B． | （1，2） | C． | （$\frac{3}{2}$，3） | D． | （2，3） |
分析 处理一元三次函数的零点问题可借助其导函数．如本题有两个不同的零点即为其导函数有两个不同的根．
解答 解：∵函数f（x）有且仅有两个不同的零点，
∴f（x）的导函数f′（x）=3x2-6bx，有两个不同的根
由f′（x）=0得x=0或x=2b
∵f（0）=a≠0，
∴f（2b）=0，即$\frac{1}{2}$＜b＜1
则f（x）有一根是确定的，为2b．
f（x）的另一个根为负的，且f（x）=（x-2b）2（x+b）
∴另一个根为-b．
则|x1-x2|=3b
∴两个根的差的绝对值为（$\frac{3}{2}$，3）
故选：C．
点评 本题考查函数求导，及一元二次导函数求根．需要熟练掌握原函数与导函数的关系，由于是选择题，本题属于中档题．
练习册系列答案
相关题目
7．
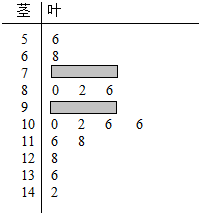某数学老师对本校2013届高三学生的高考数学成绩按1：200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：
（1）求表中a，b的值
（2）求分数在[90，100）范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90，150）内为及格）；
（3）从成绩在[100，130）范围内的学生中随机选4人，求其中成绩在[100，110）内的人数最多2人的概率．
某数学老师对本校2013届高三学生的高考数学成绩按1：200进行分层抽样抽取了20名学生的成绩，并用茎叶图记录分数如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（2）求分数在[90，100）范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在[90，150）内为及格）；
（3）从成绩在[100，130）范围内的学生中随机选4人，求其中成绩在[100，110）内的人数最多2人的概率．
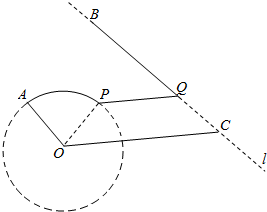如图，B、C是海岸线l上相距50km的两个海边小城，圆O是半径为10km的某海岛小城的环岛路，A为圆O上的物资中转站，其中∠AOC=$\frac{2}{3}$π，OC=25km，且l∥OA，为使中转站A的物资运往B城，计划从A地沿环岛路至某地P，再沿水路PQ至海岸线l上Q，最后沿海岸线QB至B城修建运输线，其中PQ∥OC，Q在线段BC上．
函数y=Asin（ωx+φ）（A＞0，ω＞0）的图象的一部分如图所示：