题目内容
已知cos(
+α)=-
,且α是第二象限角,则sin(α-
)的结果是 .
| π |
| 2 |
| 3 |
| 5 |
| 3π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用诱导公式求得sinα,结合α的范围利用同角三角函数的基本关系求得cosα,再根据sin(α-
)=cosα,计算求得结果.
| 3π |
| 2 |
解答:
解:∵cos(
+α)=-
=-sinα,∴sinα=
.
又∵α是第二象限角,∴cosα=-
.
则sin(α-
)=-sin(
-α)=cosα=-
,
故答案为:-
.
| π |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
又∵α是第二象限角,∴cosα=-
| 4 |
| 5 |
则sin(α-
| 3π |
| 2 |
| 3π |
| 2 |
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:本题主要考查同角三角函数的基本关系,利用诱导公式进行化简求值,属于基础题.

练习册系列答案
相关题目
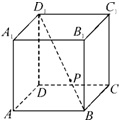 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有