题目内容
7.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1的焦点到其渐近线的距离为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
分析 根据题意,由双曲线的方程可得其焦点坐标以及渐近线方程,进而由点到直线的距离公式计算可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1,
则其焦点坐标为(±$\sqrt{7}$,0),渐近线方程为:y=±$\frac{\sqrt{3}}{2}$x,即$\sqrt{3}x$±2y=0,
则其焦点到渐近线的距离d=$\frac{|\sqrt{3}×\sqrt{7}|}{\sqrt{4+3}}$=$\sqrt{3}$;
故选:C.
点评 本题考查双曲线的几何性质,关键是求出双曲线的焦点坐标以及渐近线方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设全集U=R,若集合A={x|$\frac{x-1}{4-x}$≥0},B={x|log2x≤2},则A∩B=( )
| A. | {x|x<4} | B. | {x|x≤4} | C. | {x|1≤x<4} | D. | {x|1≤x≤4} |
18.设定义在R上的可导函数f(x)的导函数为f′(x),若f(3)=1,且3f(x)+xf′(x)>ln(x+1),则不等式(x-2017)3f(x-2017)-27>0的解集为( )
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
15.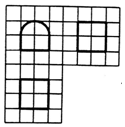 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )| A. | 10+2π | B. | 12+3π | C. | 20+4π | D. | 16+5π |
12.在平面直角坐标系xOy中,已知圆C:(x-a)2+(y-a-2)2=1,点A(0,3),若圆C上存在点M,满足|MA|=2|MO|(O为坐标原点),则实数a的取值范围是( )
| A. | [-3,0] | B. | (-∞,-3]∪[0,+∞) | C. | [0,3] | D. | (-∞,0]∪[3,+∞) |
19.若0<x<y<1,则( )
| A. | 3y<3x | B. | log0.5x<log0.5y | C. | cosx<cosy | D. | sinx<siny |
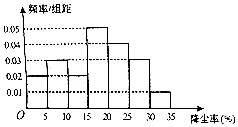 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图: