题目内容
11.已知实数x,y满足$\left\{\begin{array}{l}x+y≤6\\ x-y≤2\\ x≥0\\ y≥0\end{array}\right.$,则z=2x+y的最大值是( )| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x+y≤6\\ x-y≤2\\ x≥0\\ y≥0\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x-y=2}\\{x+y=6}\end{array}\right.$,解得A(4,2),
化目标函数z=2x+y为y=-2x+z,由图可知,当直线y=-2x+z过A时,直线在y轴上的截距最大,z有最大值为10.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.若0<x<y<1,则( )
| A. | 3y<3x | B. | log0.5x<log0.5y | C. | cosx<cosy | D. | sinx<siny |
6.已知二元一次方程组的增广矩阵为$(\begin{array}{l}{m}&{4}&{m+2}\\{1}&{m}&{m}\end{array})$,若此方程组无实数解,则实数m的值为( )
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
3.已知集合A={x|x2-1=0},B={-1,2,5},则A∩B=( )
| A. | {-1,2} | B. | {-1} | C. | {-1,5} | D. | ∅ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦距为4$\sqrt{5}$,渐近线方程为2x±y=0,则双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{64}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{16}=1$ |
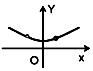
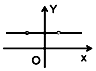
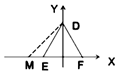 如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )
如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )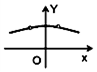

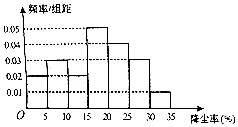 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图: