题目内容
5.设函数f(x)=x2-|x2-mx-4|(m为常数)x∈[-4,4],f(x)经过点(2,4).(1)求m的值,并画出f(x)的图象;
(2)求函数f(x)的最大值与最小值.
分析 (1)由题意知f(2)=4-|4-2m-4|=4,解得m=0,从而f(x)=x2-|x2-4|=$\left\{\begin{array}{l}{4,-4≤x≤-2或2≤x≤4}\\{2{x}^{2}-4,-2<x<2}\end{array}\right.$,由此能画出函数的图象
(2)结合图象能求出函数f(x)的最大值和最小值.
解答 解:(1)∵函数f(x)=x2-|x2-mx-4|(m为常数)x∈[-4,4],f(x)经过点(2,4),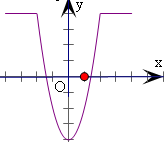
∴由题意可得f(2)=4,即f(2)=4-|4-2m-4|=4,解得m=0;
∴f(x)=x2-|x2-4|,
当x2-4≥0,解得x≥2或x≤-2,
由-4≤x≤4,即有-4≤x≤-2或2≤x≤4,
可得f(x)=x2-(x2-4)=4,为常数函数;
当x2-4<0,解得-2<x<2,
由-4≤x≤4,即有-2<x<2,
可得f(x)=x2-(4-x2=2x2-4,
单调减区间为(-2,0),增区间为(0,2),
∴f(x)=$\left\{\begin{array}{l}{4,-4≤x≤-2或2≤x≤4}\\{2{x}^{2}-4,-2<x<2}\end{array}\right.$,
画出函数的图象,如右图.
(2)由(1)结合图象得:
当x=0时,函数f(x)取最小值f(x)min=f(0)=2×02-4=-4.
当-4≤x≤-2或2≤x≤4时,函数f(x)取最大值f(x)max=4.
点评 本题考查实数值的求法,考查函数图象的作法,考查函数的最大值与最小值的求法,考查函数性质、函数图象、函数最值等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想、分类与整合思想,是中档题.

练习册系列答案
相关题目
16.在约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$下,函数z=3x-y的最小值是( )
| A. | 9 | B. | 1 | C. | -3 | D. | -9 |
14.在棱长为a的正方体ABCD-A1B1C1D1内有一个内切球O,过正方体中两条互为异面直线的AA1,BC的中点P、Q作直线,该直线被球面截在球内的线段的长为( )
| A. | $\frac{\sqrt{2}}{2}$a | B. | $\frac{1}{2}$a | C. | $\frac{1}{4}$a | D. | ($\sqrt{2}$-1)a |
15.已知 $cos({\frac{π}{2}-α})=\frac{2}{3}$,则sin(π+α)=( )
| A. | $-\frac{{\sqrt{5}}}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |