题目内容
20.函数f(x)=1+logax(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,则m+n=2.分析 由题意得点A(1,1),由此利用点A在直线mx+ny-2=0上,能求出m+n.
解答 解:∵函数f(x)=1+logax(a>0,a≠1)的图象恒过定点A,
∴点A(1,1),
∵点A在直线mx+ny-2=0上,
∴m+n-2=0,
∴m+n=2.
故答案为:2.
点评 本题考查两数和的求法,是基础题,解题时要认真审题,注意对数性质、运算法则的合理运用.

练习册系列答案
相关题目
7.以下程序运行的结果是( )
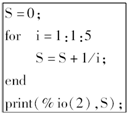
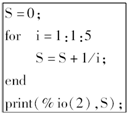
| A. | $\frac{137}{60}$ | B. | $\frac{133}{60}$ | C. | $\frac{131}{60}$ | D. | $\frac{121}{60}$ |
8.已知数列{an}满足an+1+(-1)nan=2n-1,则数列{an}的前32项之和为( )
| A. | 448 | B. | 528 | C. | 548 | D. | 608 |
15.汽车尾气是空气污染的主耍来源之一,国家明确规定,根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调査了100人,所得数据制成如下列联表:
(1)若从这100人中任选1人,选到了解机动车强制报废标准的人的概率为$\frac{3}{5}$,请将列联表中的字母用数字替换,并填写完整;
(2)在(1)的条件下,能否有95%的把握认为“对机动车强制报废标准是否了解与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(n=a+b+c+d)
临界值表:
| 不了解 | 了解 | 总计 | |
| 女性 | 25 | b | 50 |
| 男性 | c | 35 | 50 |
| 总计 | x | y | 100 |
(2)在(1)的条件下,能否有95%的把握认为“对机动车强制报废标准是否了解与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,(n=a+b+c+d)
临界值表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |