题目内容
5．已知数列{an}为等比数列，an＞0，a1=2，2a2+a3=30．（Ⅰ）求an；
（Ⅱ）若数列{bn}满足，bn+1=bn+an，b1=a2，求b5=？
分析 （Ⅰ）由题意，{an}为等比数列，a1=2，2a2+a3=30．即可求出q，可得an；
（Ⅱ）根据bn+1=bn+an，b1=a2，依次递推计算b2，b3，b4可得b5的值．
解答 解：（Ⅰ）由题意，{an}为等比数列，a1=2，2a2+a3=30．设公比为q，an＞0．
可得：4q+2q2=30，
解得：q=3或-5（舍去）
∴an=2•3n-1
（Ⅱ）由b1=a2，
∴b1=2×3=6．
bn+1=bn+an，
∴b2=b1+a1=2+6=8．
b3=b2+a2=8+6=14．
b4=b3+a3=14+18=32．
b5=b4+a4=32+54=86．
点评 本题考查了等比数列的通项公式的求法和根据数列的递推公式写出数列的前几项．属于基础题．
练习册系列答案
相关题目
15．
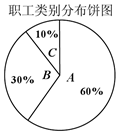某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金．保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）．
对于A、B、C三类工种职工每人每年保费分别为a元，a元，b元，出险后的赔偿金额分别为100万元，100万元，50万元，保险公司在开展此项业务过程中的固定支出为每年10万元．
（Ⅰ）若保险公司要求利润的期望不低于保费的20%，试确定保费a、b所要满足的条件；
（Ⅱ）现有如下两个方案供企业选择；
方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；
方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付．
若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a、b所要满足的条件，并判断企业是否可与保险公司合作．（若企业选择方案2的支出低于选择方案1的支出期望，且与（Ⅰ）中保险公司所提条件不矛盾，则企业可与保险公司合作．）
某保险公司针对一个拥有20000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金．保险公司把企业的所有岗位共分为A、B、C三类工种，从事三类工种的人数分布比例如图，根据历史数据统计出三类工种的赔付频率如下表（并以此估计赔付频率）．| 工种类别 | A | B | C |
| 赔付频率 | $\frac{1}{1{0}^{5}}$ | $\frac{2}{1{0}^{5}}$ | $\frac{1}{1{0}^{4}}$ |
（Ⅰ）若保险公司要求利润的期望不低于保费的20%，试确定保费a、b所要满足的条件；
（Ⅱ）现有如下两个方案供企业选择；
方案1：企业不与保险公司合作，企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工；
方案2：企业与保险公司合作，企业负责职工保费的60%，职工个人负责保费的40%，出险后赔偿金由保险公司赔付．
若企业选择方案2的支出（不包括职工支出）低于选择方案1的支出期望，求保费a、b所要满足的条件，并判断企业是否可与保险公司合作．（若企业选择方案2的支出低于选择方案1的支出期望，且与（Ⅰ）中保险公司所提条件不矛盾，则企业可与保险公司合作．）
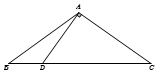如图，在△ABC中，已知点D在BC边上，AD⊥AC，AB=2$\sqrt{5}$，sin∠BAC=$\frac{{\sqrt{5}}}{3}$，AD=3，则BD的长为3．
如图，长方体ABCD-A1B1C1D1中，点M在棱BB1上，两条直线MA，MC与平面ABCD所成角均为θ，AC与BD交于点O．