题目内容
9．某地实行高考改革，考生除参加语文，数学，外语统一考试外，还需从物理，化学，生物，政治，历史，地理六科中选考三科，要求物理，化学，生物三科至少选一科，政治，历史，地理三科至少选一科，则考生共有多少种选考方法（ ）| A． | 6 | B． | 12 | C． | 18 | D． | 24 |
分析 根据题意，分2种情况讨论：①、从物理，化学，生物三科中选2科，从政治，历史，地理三科中选1科，②、从物理，化学，生物三科中选1科，从政治，历史，地理三科中选2科，分别求出每一种情况下的选法数目，由分类计数原理计算可得答案．
解答 解：根据题意，分2种情况讨论：
①、从物理，化学，生物三科中选2科，从政治，历史，地理三科中选1科，
则有C32•C31=9种选法；
②、从物理，化学，生物三科中选1科，从政治，历史，地理三科中选2科，
则有C32•C31=9种选法；
则一共有9+9=18种选考方法；
故选：C．
点评 本题考查排列、组合的应用，分类讨论注意不能有重复和遗漏的情况．
练习册系列答案
相关题目
20．若偶函数f（x）满足f（x）=$\left\{{\begin{array}{l}{x-1+ln3-ln（2x+1），0＜x≤\frac{1}{2}}\\{\frac{（x+1）（x+2）（x+3）ln（2x-1）}{3x+5}，x＞\frac{1}{2}}\end{array}}$则曲线y=f（x）在点（-1，0）处的切线方程为（ ）
| A． | 6x-y+6=0 | B． | x-3y+1=0 | C． | 6x+y+6=0 | D． | x+3y+1=0 |
1．
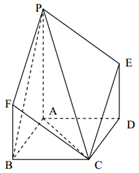如图，点P是菱形ABCD所在平面外一点，PA⊥平面ABCD，PA∥FB∥ED，∠ABC=60°，PA=AB=2BF=2DE．
（Ⅰ）求证：平面PAC⊥平面PCE；
（Ⅱ）求二面角B-PC-F的余弦值．
如图，点P是菱形ABCD所在平面外一点，PA⊥平面ABCD，PA∥FB∥ED，∠ABC=60°，PA=AB=2BF=2DE．（Ⅰ）求证：平面PAC⊥平面PCE；
（Ⅱ）求二面角B-PC-F的余弦值．
18．如图是八位同学400米测试成绩的茎叶图（单位：秒），则（ ）
| A． | 平均数为64 | B． | 众数为7 | C． | 极差为17 | D． | 中位数为64.5 |