题目内容
19.已知抛物线y2=4x上一点A到焦点F的距离为3,则点A的坐标为(2,±2$\sqrt{2}$).分析 根据题意,由抛物线的方程可得其焦点坐标以及准线方程,设所求点坐标为P(x,y),作PQ⊥l于Q,由抛物线的定义分析可得P到准线的距离等于P、Q的距离,即x+1=3,解可得x的值,将x的值代入抛物线方程即可得y的值,综合即可得答案.
解答  解:∵抛物线方程为y2=4x,∴焦点为F(1,0),
解:∵抛物线方程为y2=4x,∴焦点为F(1,0),
准线为l:x=-1.
设所求点坐标为P(x,y),作PQ⊥l于Q.
根据抛物线定义可知P到准线的距离等于P、Q的距离,
即x+1=3,
解之得x=2,代入抛物线方程求得y=±2$\sqrt{2}$,
∴点P坐标为:(2,±2$\sqrt{2}$).
故答案为:(2,±2$\sqrt{2}$).
点评 本题考查抛物线的几何性质,关键是利用抛物线的几何性质进行转化.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
9.某地实行高考改革,考生除参加语文,数学,外语统一考试外,还需从物理,化学,生物,政治,历史,地理六科中选考三科,要求物理,化学,生物三科至少选一科,政治,历史,地理三科至少选一科,则考生共有多少种选考方法( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
14.某产品的广告费用x与销售额y的统计数据如表:
用最小二乘法算得的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\widehat{b}$为7,据此预测广告费用为6万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
10.一组数据的平均数是4.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A. | 55.2,3.6 | B. | 55.2,56.4 | C. | 64.8,63.6 | D. | 64.8,3.6 |
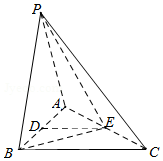 如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$
如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$