题目内容
在等差数列{an}中，a4=2-a3，则此数列{an}的前6项和为（ ）
| A、12 | B、3 | C、36 | D、6 |
考点：等差数列的前n项和,等差数列的通项公式
专题：等差数列与等比数列
分析：由题意和等差数列的性质可得a1+a6=a3+a4=2，而由求和公式可得S6=3（a1+a6），代值计算可得．
解答：
解：∵在等差数列{an}中，a4=2-a3，
∴a3+a4=2，∴a1+a6=a3+a4=2，
∴数列{an}的前6项和S6=
=3（a1+a6）=6
故选：D
∴a3+a4=2，∴a1+a6=a3+a4=2，
∴数列{an}的前6项和S6=
| 6(a1+a6) |
| 2 |
故选：D
点评：本题考查等差数列的通项公式和求和公式，涉及等差数列的性质，属基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
“a=-1”是“（a-i）2”为纯虚数的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数y=ax-b（a＞0且a≠1）的图象经过第一、三、四象限，则（ ）
| A、0＜a＜1，b＞1 |
| B、0＜a＜1，b＜1 |
| C、a＞1，b＞1 |
| D、a＞1，b＜1 |
在等差数列{an}中，已知a1=2，a2+a3=13，则a5=（ ）
| A、13 | B、14 | C、15 | D、16 |
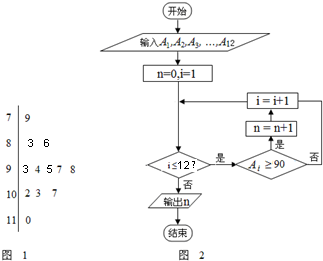图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到12次的考试成绩依次记为A1，A2，…，A12．图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（ ）