题目内容
20.若不等式(a2+a)x2-ax+1>0对任意实数x都成立,则实数a的取值范围是{x|-$\frac{4}{3}$<a<-1或a=0}.分析 根据题意,令f(x)=(a2+a)x2-ax+1,分析可得f(x)min>0;对二次项系数分2种情况讨论:①、a2+a=0,②、a2+a≠0,结合函数的性质分析可得a的取值范围,综合即可得答案.
解答 解:根据题意,令f(x)=(a2+a)x2-ax+1,
若不等式(a2+a)x2-ax+1>0对任意实数x都成立,则有函数f(x)min>0;
分2种情况讨论:
①、a2+a=0,即a=0或-1时,
其中当a=0时,f(x)=1,不等式为1>0,恒成立,符合题意;
当a=-1时,不等式为x+1>0,不符合题意;
②、a2+a≠0,f(x)=(a2+a)x2-ax+1为二次函数;
若函数f(x)min>0,必有$\left\{\begin{array}{l}{{a}^{2}+a>0}\\{△={a}^{2}-4({a}^{2}+a)<0}\end{array}\right.$,解可得-$\frac{4}{3}$<a<-1;
综合可得:实数a的取值范围是{x|-$\frac{4}{3}$<a<-1或a=0};
故答案为:{x|-$\frac{4}{3}$<a<-1或a=0}.
点评 本题考查二次函数的性质,涉及不等式的恒成立问题,注意要对二次项系数进行讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
5.已知A,B是锐角三角形ABC的两个内角,设m=tanA•tanB,f(x)=logmx,则下列各式一点成立的是( )
| A. | f(cosA)>f(sinB) | B. | f(sinA)>f(cosB) | C. | f(cosA)≥f(sinB) | D. | f(sinA)≥f(cosB) |
 的前
的前 项之和为
项之和为 满足
满足 .
. 的通项公式;
的通项公式; 的前
的前 .
. 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称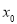 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.