题目内容
8. 如图是正方体的平面展开图,在这个正方体中,
如图是正方体的平面展开图,在这个正方体中,①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A. | ③ | B. | ③④ | C. | ①③ | D. | ①③④ |
分析 把正方体的平面展开图还原成正方体ABCA-EFMN,由此能求出结果.
解答 解:把正方体的平面展开图还原成正方体ABCA-EFMN,
得:对于①,BM与ED不平行,故①不正确;
对于②,CN∥BE,故②不正确;
对于③,∵BE∥CN,在等边三角形EBM中,可得∠EBM=60°,即CN与BM成60°角,故③正确;
对于④,∵BN在平面NDCM上的投影为CN,根据三垂线定理得DM与BN垂直,故④正确.
正确命题的序号是③④.故选:B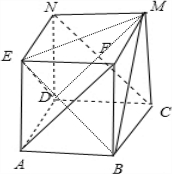
点评 本本题考查正方体的结构特征,异面直线的判定,异面直线及其所成的角,空间中直线与直线之间的位置关系,几何体的折叠与展开,考查空间想象能力,是中档题..

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
17.设m,n∈R,若直线mx+ny=2与圆x2+y2=1相切,则m+n的取值范围是( )
| A. | [-2,2] | B. | [-∞,-2]∪[2,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
3.已知点A(-1,0),B(1,0),若圆x2+y2-8x-6y+25-m=0上存在点P使$\overrightarrow{PA}•\overrightarrow{PB}=0$,则m的最小值为16.
17.函数f(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后得到的函数是奇函数,则函数f(x)的图象( )
| A. | 关于点(-$\frac{π}{3}$,0)对称 | B. | 关于直线x=-$\frac{π}{6}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
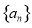 的前
的前 项和为
项和为 ,且
,且 ,在区间
,在区间 内任取一个实数作为数列
内任取一个实数作为数列 的最小值为
的最小值为 的概率为( )
的概率为( ) B.
B.  C.
C. 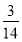 D.
D.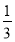
 如图,在平面四边形ABCD中,若AB=1,BC=$\sqrt{2}$,AD=$\sqrt{2}$DC,∠ACD=90°,则对角线BD的最大值为3.
如图,在平面四边形ABCD中,若AB=1,BC=$\sqrt{2}$,AD=$\sqrt{2}$DC,∠ACD=90°,则对角线BD的最大值为3. 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆B的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆B的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题: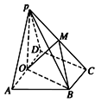 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PDA⊥底面ABCD,O是AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.