题目内容

求函数
lim
x→0
cosx-1
x
的极限．
考点：极限及其运算
专题：
分析：因为当x→0时，分子、分母的值都是0，所以采用洛必达法则使计算简便．
解答： 解：原式=
lim
x→0
(cosx-1)′
x′
=
lim
x→0
(-sinx)=0．
点评：本题考查了对于
0
0
型函数求极限的方法；利用洛必达法则可以解决
0
0
，
∞
∞
的函数求极限的问题，即对分子分母分别求导，然后求极限．
练习册系列答案
相关题目
已知点(
2
，2)在幂函数f（x）=xα（α＞0）的图象上，则f（x）的表达式是（　　）
A、f（x）=x2
B、f（x）=x-2
C、f（x）=x
1
2
D、f（x）=x-
1
2
已知a＞b＞c，且a+b+c=0，
（1）试判断a，c及2a+c的符号；
（2）用分析法证明：
b2-ac
a
＜
3
．
已知f（x）=3x2-12x+5，当f（x）的定义域为下列各区间时，求函数的最大值和最小值．
（1）[0，3]；
（2）[-1，1]；
（3）[3，+∞）．
讨论关于x的方程|x2-4x+3|-a=x的根的个数．
已知A（-2，
3
）和椭圆E：
x2
16
+
y2
12
=1，F是椭圆左焦点，一动点M在椭圆上移动，求|AM|+|FM|的最小值．
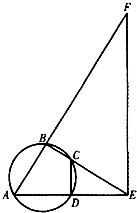如图，A、B、C、D四点共圆，BC和AD的延长线交于点E，点F在AB的延长线上．
（Ⅰ）若EA=2ED，CE=2BC，求
AB
CD
的值；
（Ⅱ）若EF∥CD，求证：线段FA、FE、FB成等比数列．
如图，五面体中，四边形ABCD是矩形，DA⊥平面ABEF，且DA=1，AB∥EF，AB=
1
2
EF=2
2
，AF=BE=2，M为EF的中点．
（Ⅰ）求证：AM⊥平面ADF；
（Ⅱ）求二面角A-DF-E的平面角的余弦值．
设函数f（x）=x3-3ax+b（a≠0）．
（1）若曲线y=f（x）在点（2，f（x））处与直线y=8相切，求a，b的值；
（2）求函数f（x）的单调区间与极值点．
（3）设函数f（x）的导函数是f′（x），当a=1时求证：对任意x1，x2∈（3，+∞），|f（x1）-f（x2）|≥|f′（x1）-f′（x2）|成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网