题目内容
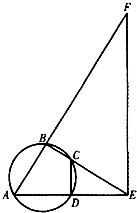如图，A、B、C、D四点共圆，BC和AD的延长线交于点E，点F在AB的延长线上．（Ⅰ）若EA=2ED，CE=2BC，求
| AB |
| CD |
（Ⅱ）若EF∥CD，求证：线段FA、FE、FB成等比数列．
考点：与圆有关的比例线段
专题：立体几何
分析：（Ⅰ）由A，B，C，D四点共圆，得∠CDE=∠ABE，得△ABE∽△CDE，由此能求出
．
（Ⅱ）由EF∥CD，得推导出△BEF∽△EAF，由此能证明FA，FE，FB成等比数列．
| AB |
| CD |
（Ⅱ）由EF∥CD，得推导出△BEF∽△EAF，由此能证明FA，FE，FB成等比数列．
解答：
（Ⅰ）解：由A，B，C，D四点共圆，得∠CDE=∠ABE，
又∠DEC=∠BEA，
∴△ABE∽△CDE，
∴
=
=
，①
设DE=a，CE=b，
则由
=
，得3b2=2a2，即b=
a，
代入①，得
=
=
．
（Ⅱ）证明：由EF∥CD，得∠AEF=∠CDE，
又∠BFE=∠EFA，
∴△BEF∽△EAF，
∴
=
，
∴FA，FE，FB成等比数列．
又∠DEC=∠BEA，
∴△ABE∽△CDE，
∴
| AB |
| CD |
| BE |
| DE |
| AE |
| CE |
设DE=a，CE=b，
则由
| BE |
| DE |
| AE |
| CE |
| ||
|
代入①，得
| AB |
| CD |
| 3b |
| a |
| 6 |
（Ⅱ）证明：由EF∥CD，得∠AEF=∠CDE，
又∠BFE=∠EFA，
∴△BEF∽△EAF，
∴
| FA |
| FE |
| FE |
| FB |
∴FA，FE，FB成等比数列．
点评：本题考查两线段比值的求法，考查三条线段长成等比数列的证明，解题时要认真审题，注意三角形相似的性质的合理运用．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
等比数列{an}的各项均为正数，且a2a18=
，则log3a1+log3a3+log3a5+…+log3a19=（ ）
| 1 |
| 3 |
| A、5 | ||
| B、-5 | ||
C、
| ||
D、
|
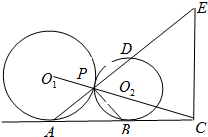如图，已知⊙O1与⊙O2外切于点P，AB是两圆的外公切线，A，B为切点，AB与O1O2 的延长线相交于点C，延长AP交⊙O2于点D，点E在AD延长线上．