Question

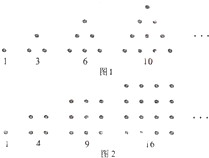古希腊人常用小石子在沙滩上摆成各种形状研究数，如他们研究过图1中的1，3，6，10，…，由于这些数能表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16…这样的数为正方形数，则除1外，最小的既是三角形数又是正方形数的是

 

．

Answer 1

考点：归纳推理

专题：规律型,推理和证明

分析：图1中求出1、3、6、10，…，第n个图中点的个数是1+2+3+…+n，即

n(n+1)

2

；图2中1、4、9、16，…，第n个图中点的个数是n²．求出能同时满足两个式子的数，即可得到答案．

解答： 解：∵两个相邻的三角形数的和是正方形数，
故4=1+3，但4不是三角形数，
9=3+6，但9不是三角形数；
16=6+10，但16不是三角形数；
25=10+15，但25不是三角形数；
36=15+21，36是三角形数；
故除1外，最小的既是三角形数又是正方形数的是36，
故答案为：36

点评：本题考查的知识点是归纳推理，其中分析出两个相邻的三角形数的和是正方形数，进而逐一列举是解答的关键．