题目内容
已知盒子里有大小质地相同的红、黄、白球各一个,从中有放回的抽取9次,每次抽一个球,则抽到黄球的次数的期望n= ,估计抽到黄球次数恰好为n次的概率 50%(填大于或小于)
考点:离散型随机变量的期望与方差,n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:由题意知,取到黄球的次数X~B(9,
),抽到黄球次数恰好为n次的概率p=
(
)n(1-
)9-n,由此能求出结果.
| 1 |
| 3 |
| C | n 9 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:由题意知,每次取到黄球的概率均为
,
则取到黄球的次数X~B(9,
),
∴n=EX=9×
=3.
抽到黄球次数恰好为n次的概率p=
(
)n(1-
)9-n<0.5.
故答案为:3,小于.
| 1 |
| 3 |
则取到黄球的次数X~B(9,
| 1 |
| 3 |
∴n=EX=9×
| 1 |
| 3 |
抽到黄球次数恰好为n次的概率p=
| C | n 9 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:3,小于.
点评:本题考查离散型随机变量的数学期望的求法,考查概率的估计值,是中档题,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
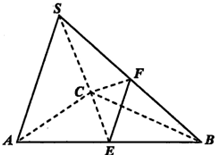 在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,
在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,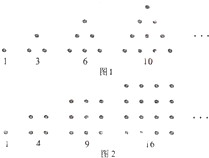 古希腊人常用小石子在沙滩上摆成各种形状研究数,如他们研究过图1中的1,3,6,10,…,由于这些数能表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数为正方形数,则除1外,最小的既是三角形数又是正方形数的是
古希腊人常用小石子在沙滩上摆成各种形状研究数,如他们研究过图1中的1,3,6,10,…,由于这些数能表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数为正方形数,则除1外,最小的既是三角形数又是正方形数的是