题目内容
18.已知sinα+sinβ=$\frac{\sqrt{2}}{2}$,求cosα+cosβ的最大值和最小值.分析 cosα+cosβ=t,和已知式子两式平方相加结合三角函数的值域可得t的不等式,解不等式可得.
解答 解:设cosα+cosβ=t,两式平方相加可得:
sin2α+2sinαsinβ+sin2β+cos2α+2cosαcosβ+cos2β=$\frac{1}{2}$+t2,
∴2+2(sinαsinβ+cosαcosβ)=$\frac{1}{2}$+t2,
∴2+2cos(α-β)=$\frac{1}{2}$+t2,
∴cos(α-β)=$\frac{1}{2}$t2-$\frac{3}{4}$∈[-1,1],
解不等式可得-$\frac{\sqrt{14}}{2}$≤t≤$\frac{\sqrt{14}}{2}$,
∴cosα+cosβ的最大值和最小值分别为$\frac{\sqrt{14}}{2}$,-$\frac{\sqrt{14}}{2}$.
点评 本题考查三角函数恒等变换,涉及三角函数的值域和不等式的解法,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.设集合A={x|y=$\sqrt{2x{-x}^{2}}$.x∈N},B={x|y=ln(2-x)},则A∩B表示的集合为( )
| A. | {1} | B. | {x|0≤x<2} | C. | {0,1} | D. | {0,1,2} |
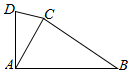 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=150°,∠BAC=60°,AC=2,AB=$\sqrt{3}$+1.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=150°,∠BAC=60°,AC=2,AB=$\sqrt{3}$+1.