题目内容
7．已知p：|x-a|≤4，q：$\frac{1}{5x-{x}^{2}-6}$≥0，q是p的充分不必要条件，求实数a的取值范围．分析 p：|x-a|≤4，解得a-4≤x≤a+4．q：$\frac{1}{5x-{x}^{2}-6}$≥0，化为x2-5x+6＜0，解得x范围．再利用q是p的充分不必要条件即可得出．
解答 解：p：|x-a|≤4，解得a-4≤x≤a+4．
q：$\frac{1}{5x-{x}^{2}-6}$≥0，∴5x-x2-6＞0，化为x2-5x+6＜0，解得2＜x＜3．
∵q是p的充分不必要条件，
∴$\left\{\begin{array}{l}{a-4≤2}\\{3≤a+4}\end{array}\right.$，解得-1≤a≤6．
∴实数a的取值范围是[-1，6]．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．函数y=$\frac{x-2}{2x-1}$（x≠$\frac{1}{2}$）的反函数是（ ）
| A． | y=$\frac{2x-1}{x+2}$（x≠-2） | B． | y=$\frac{x-2}{2x-1}$（x≠$\frac{1}{2}$） | C． | y=$\frac{x+1}{2x-1}$（x≠$\frac{1}{2}$） | D． | y=$\frac{2x-1}{x-2}$（x≠2） |
15．若a＞0，b＞0，且a+b=1，则$\frac{2}{a}$+$\frac{2}{b}$的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | 8 | D． | 16 |
2．如果点P（x，y）在圆（x-3）2+（y+4）2=25上，则x-y的最大值是（ ）
| A． | 10 | B． | 12 | C． | 5+3$\sqrt{2}$ | D． | 7+5$\sqrt{2}$ |
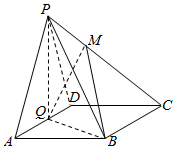如图，在四棱锥P-ABCD中，底面ABCD为棱形，∠BAD=60°，Q为AD的中点．
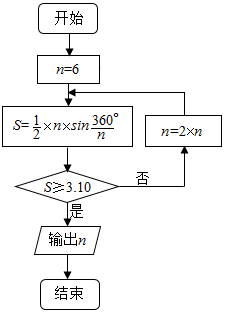公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为24．（参考数据：sin15°=0.2588，sin7.5°=0.1305）