题目内容
6.某公共汽车有A,B路路车,A路车每4分钟一班,B路车每6分钟一班,求满足下列条件的概率:(1)一个乘客坐A路车时,候车时间不超过2分钟的概率;
(2)一位想乘A路汽车的乘客来到该站并盼望下一辆是A路车,试求下一辆是A路车的概率;
(3)在两分钟内有一辆汽车到达的概率.
分析 (1)由A路车每4分钟一班,且一乘客等车的任一时刻是等可能的,由几何概型公式得到结果.
(2)把等待A路的时间设为x,则x的取值范围是[0,4],同理把等待B路的时间设为y,则y的取值范围是[0,6],建立直角坐标系,并在坐标系里画出x,y围成的区域,根据几何概型的概率的公式计算即可,
(3)2分钟内有车到达也就说0<x<2或0<y<2同样画出相应的区域,求其面积,几何概型的概率的公式计算即可
解答  解:(1)由题意知本题是一个几何概型,试验包含的所有事件是A路车每4分钟一班,时间长度是4,
解:(1)由题意知本题是一个几何概型,试验包含的所有事件是A路车每4分钟一班,时间长度是4,
而满足条件的事件是候车时间不超过2分钟长度是2,
由几何概型概率公式得到P=$\frac{2}{4}$=$\frac{1}{2}$,
(2)把等待A路的时间设为x,则x的取值范围是[0,4]
同理把等待B路的时间设为y,则y的取值范围是[0,6]
建立直角坐标系,并在坐标系里画出x,y围成的区域(是一个边长分别为4,6的矩形,面积为24)
若下一辆是A车的话就是说A比B要先到,也就是等待A路的时间x小于等待B路的时间y
画出y>x在矩形表示的区域,其面积为16,
所以概率$\frac{16}{24}$=$\frac{2}{3}$,
(3)2分钟内有车到达也就说0<x<2或0<y<2同样画出相应的区域,如图所示
落在矩形内部的面积为2×4+2×6-2×2=16 所以概率$\frac{16}{24}$=$\frac{2}{3}$
点评 本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现,有时文科会考这种类型的解答题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 12 |
17.函数y=$\frac{x-2}{2x-1}$(x≠$\frac{1}{2}$)的反函数是( )
| A. | y=$\frac{2x-1}{x+2}$(x≠-2) | B. | y=$\frac{x-2}{2x-1}$(x≠$\frac{1}{2}$) | C. | y=$\frac{x+1}{2x-1}$(x≠$\frac{1}{2}$) | D. | y=$\frac{2x-1}{x-2}$(x≠2) |
15.若a>0,b>0,且a+b=1,则$\frac{2}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 8 | D. | 16 |
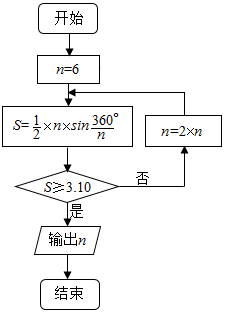 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为24.(参考数据:sin15°=0.2588,sin7.5°=0.1305)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为24.(参考数据:sin15°=0.2588,sin7.5°=0.1305)