题目内容
9.复数$\frac{1}{\sqrt{1-{x}^{2}}}$+(2-2x)i(x∈R)在复平面内的对应点位于第一象限.分析 先求出x的范围,再判断虚部和实部的符合,利用几何意义即可得出.
解答 解:∵1-x2>0,
∴-1<x<1,
∴$\frac{1}{2}$<2x<2,
∴0<2-2x<$\frac{3}{2}$,
∵$\frac{1}{\sqrt{1-{x}^{2}}}$>0,
∴复数$\frac{1}{\sqrt{1-{x}^{2}}}$+(2-2x)i(x∈R)在复平面内的对应点位于第一象限,
故答案为:一.
点评 本题考查了指数函数的值域和不等式的解集和复数的何意义,属于基础题.

练习册系列答案
相关题目
19.(1-x2)4($\frac{x+1}{x}$)5的展开式中$\frac{1}{x}$的系数为( )
| A. | 5 | B. | 11 | C. | -21 | D. | -29 |
17.函数y=$\frac{x-2}{2x-1}$(x≠$\frac{1}{2}$)的反函数是( )
| A. | y=$\frac{2x-1}{x+2}$(x≠-2) | B. | y=$\frac{x-2}{2x-1}$(x≠$\frac{1}{2}$) | C. | y=$\frac{x+1}{2x-1}$(x≠$\frac{1}{2}$) | D. | y=$\frac{2x-1}{x-2}$(x≠2) |
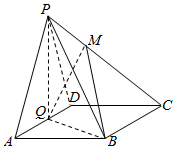 如图,在四棱锥P-ABCD中,底面ABCD为棱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为棱形,∠BAD=60°,Q为AD的中点.