题目内容
 如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若
如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若| AC |
| DE |
| AP |
①若点E和A重合,点P和B重合,则x=-1,y=1;
②若点E是线段AB的中点,则点P是圆弧
 |
| DB |
③若点E和B重合,且点P为靠近D点的圆弧的三等分点,则x+y=3;
④若点E与B重合,点P为
 |
| DB |
考点:命题的真假判断与应用
专题:数形结合,转化思想,平面向量及应用,圆锥曲线的定义、性质与方程
分析:以AB为x轴,AD为y轴建立直角坐标系,设正方形ABCD的边长为1,
①,若点E和A重合,点P和B重合,可求得E、P的坐标及向量
=(0,-1),
=(1,0),利用
=x
+y
(xy≠0)及向量的坐标运算可求得x=-1,y=1,从而可判断①;
②,若点E是线段AB的中点,点P是圆弧
的中点,同理可求得
,此方程组无解,从而可判断②;
③,若点E和B重合,且点P为靠近D点的圆弧的三等分点,可求得x+y=
,可判断③;
④,若点E与B重合,点P(a,b)为
上任一点,
=x
+y
⇒(1,1)=x(1,-1)+y(a,b),利用a2+b2=1可得:
+
=1,整理得:
-x2=1,
从而可判断④.
①,若点E和A重合,点P和B重合,可求得E、P的坐标及向量
| DE |
| AP |
| AC |
| DE |
| AP |
②,若点E是线段AB的中点,点P是圆弧
 |
| DB |
|
③,若点E和B重合,且点P为靠近D点的圆弧的三等分点,可求得x+y=
| 3 |
④,若点E与B重合,点P(a,b)为
 |
| DB |
| AC |
| DE |
| AP |
| (1-x)2 |
| y2 |
| (1+x)2 |
| y2 |
| y2 |
| 2 |
从而可判断④.
解答:
解: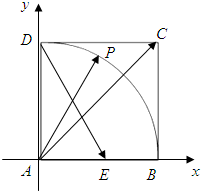 以AB为x轴,AD为y轴建立直角坐标系,设正方形ABCD的边长为1,如图,
以AB为x轴,AD为y轴建立直角坐标系,设正方形ABCD的边长为1,如图,
则A(0,0),B(1,0),C(1,1),D(0,1),
=(1,1).
因为
=x
+y
(xy≠0),
所以,对于①,若点E和A重合,点P和B重合,则E(0,0),P(1,0),
=(0,-1),
=(1,0),
=x
+y
⇒(1,1)=x(0,-1)+y(1,0),即
,故①正确;
则x=-1,y=1;
对于②,若点E是线段AB的中点,则E(
,0),
=(
,-1);若点P是圆弧
的中点,则P(cos45°,sin45°),即P(
,
),
=(
,
),
=x
+y
⇒(1,1)=x(
,-1)+y(
,
),即
,此方程组无解,
故②错误;
对于③,若点E和B重合,则E(1,0),
=(1,-1);又点P为靠近D点的圆弧的三等分点,则P(cos60°,sin60°),
即P(
,
),
=(
,
),
=x
+y
⇒(1,1)=x(1,-1)+y(
,
),即
,解得
,
则x+y=
,故③错误;
对于④,若点E与B重合,则E(1,0),
=(1,-1);
又点P(a,b)为
上任一点,则
=(a,b)(0≤a≤1,0≤b≤1,a2+b2=1),
=x
+y
⇒(1,1)=x(1,-1)+y(a,b),
即
,由a2+b2=1得:
+
=1,整理得:
-x2=1,则动点(x,y)的轨迹为双曲线的一部分,故④正确.
综上所述,说法正确的是①④,
故答案为:①④.
 以AB为x轴,AD为y轴建立直角坐标系,设正方形ABCD的边长为1,如图,
以AB为x轴,AD为y轴建立直角坐标系,设正方形ABCD的边长为1,如图,则A(0,0),B(1,0),C(1,1),D(0,1),
| AC |
因为
| AC |
| DE |
| AP |
所以,对于①,若点E和A重合,点P和B重合,则E(0,0),P(1,0),
| DE |
| AP |
| AC |
| DE |
| AP |
|
则x=-1,y=1;
对于②,若点E是线段AB的中点,则E(
| 1 |
| 2 |
| DE |
| 1 |
| 2 |
 |
| DB |
| ||
| 2 |
| ||
| 2 |
| AP |
| ||
| 2 |
| ||
| 2 |
| AC |
| DE |
| AP |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
|
故②错误;
对于③,若点E和B重合,则E(1,0),
| DE |
即P(
| 1 |
| 2 |
| ||
| 2 |
| AP |
| 1 |
| 2 |
| ||
| 2 |
| AC |
| DE |
| AP |
| 1 |
| 2 |
| ||
| 2 |
|
|
则x+y=
| 3 |
对于④,若点E与B重合,则E(1,0),
| DE |
又点P(a,b)为
 |
| DB |
| AP |
| AC |
| DE |
| AP |
即
|
| (1-x)2 |
| y2 |
| (1+x)2 |
| y2 |
| y2 |
| 2 |
综上所述,说法正确的是①④,
故答案为:①④.
点评:本题考查命题的真假判断与应用,着重考查向量的数量积的坐标运算,考查等价转化思想、方程思想与运算求解能力、作图能力,属于难题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知sinα+cosα=
,α∈(0,π),则cosα-sinα=( )
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、±
|
某几何体的三视图如图所示,则该几何体的体积是( )
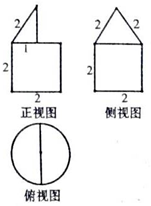

A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|