题目内容
设数列{an}的前n项和为Sn,的4Sn=an2+2an-3,且a1、a2、a3、a4…a11成等比数列,当n≥11时,an>0.
(1)求证,当a≥11时,{an}为等差数列
(2)求:当n>10时,{an}的前n项和Sn.
(1)求证,当a≥11时,{an}为等差数列
(2)求:当n>10时,{an}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由4Sn=an2+2an-3,利用递推式可得:a1=3或-1.当n≥2时,(an+an-1)(an-an-1-2)=0,可得an=-an-1,或an-an-1=2.由于a1、a2、a3、a4…a11成等比数列,当n≥11时,an>0.因此当n≤10时,取an=-an-1;当n≥11时,取an-an-1=2,必须取a1=3.
(2)当n≤10时,an=3×(-1)n-1,当n>10时,an=3+2(n-11)=2n-19.利用等差数列的前n项和公式即可得出.
(2)当n≤10时,an=3×(-1)n-1,当n>10时,an=3+2(n-11)=2n-19.利用等差数列的前n项和公式即可得出.
解答:
(1)证明:∵4Sn=an2+2an-3,∴当n=1时,4a1=
+2a1-3,解得a1=3或-1.
当n≥2时,4Sn-1=
+2an-1-3,(an+an-1)(an-an-1-2)=0,
∴an=-an-1,或an-an-1=2.
由于a1、a2、a3、a4…a11成等比数列,当n≥11时,an>0.
∴当n≤10时,取an=-an-1;当n≥11时,取an-an-1=2,必须取a1=3.
∴当a≥11时,{an}为等差数列,首项为3,公差为2.
(2)当n≤10时,an=3×(-1)n-1,
当n>10时,an=3+2(n-11)=2n-19.
{an}的前n项和Sn=(3-3+3-3+…+3-3)+3+5+…+(2n-19)
=
=n2-18n+80.
| a | 2 1 |
当n≥2时,4Sn-1=
| a | 2 n-1 |
∴an=-an-1,或an-an-1=2.
由于a1、a2、a3、a4…a11成等比数列,当n≥11时,an>0.
∴当n≤10时,取an=-an-1;当n≥11时,取an-an-1=2,必须取a1=3.
∴当a≥11时,{an}为等差数列,首项为3,公差为2.
(2)当n≤10时,an=3×(-1)n-1,
当n>10时,an=3+2(n-11)=2n-19.
{an}的前n项和Sn=(3-3+3-3+…+3-3)+3+5+…+(2n-19)
=
| (n-10)(3+2n-19) |
| 2 |
=n2-18n+80.
点评:本题考查了递推式的应用、等差数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设sinα>0,cosα<0,且sin
>cos
,则
的取值范围是( )
| α |
| 3 |
| α |
| 3 |
| α |
| 3 |
A、(2kπ+
| ||||||||
B、(
| ||||||||
C、(2kπ+
| ||||||||
D、(2kπ+
|
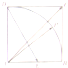 如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若
如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若