题目内容
已知sinα+cosα=
，α∈（0，π），则cosα-sinα=（ ）
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、±
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：把已知等式两边平方，利用完全平方公式及同角三角函数间的基本关系化简，整理求出2sinαcosα的值，根据α的范围判断出cosα-sinα的正负，利用完全平方公式及同角三角函数间的基本关系求出cosα-sinα的值即可．
解答：
解：把sinα+cosα=
，两边平方得：（sinα+cosα）2=1+2sinαcosα=
，
∴2sinαcosα=-
，
∵α∈（0，π），
∴sinα＞0，cosα＜0，即cosα-sinα＜0，
∴（cosα-sinα）2=1-2sinαcosα=
，
则cosα-sinα=-
，
故选：C．
| 2 |
| 3 |
| 4 |
| 9 |
∴2sinαcosα=-
| 5 |
| 9 |
∵α∈（0，π），
∴sinα＞0，cosα＜0，即cosα-sinα＜0，
∴（cosα-sinα）2=1-2sinαcosα=
| 14 |
| 9 |
则cosα-sinα=-
| ||
| 3 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
设sinα＞0，cosα＜0，且sin
＞cos
，则
的取值范围是（ ）
| α |
| 3 |
| α |
| 3 |
| α |
| 3 |
A、（2kπ+
| ||||||||
B、（
| ||||||||
C、（2kπ+
| ||||||||
D、（2kπ+
|
以点（1，0）为圆心，且过坐标原点的圆的方程为（ ）
| A、x2+y2+2x=0 |
| B、x2+y2+x=0 |
| C、x2+y2-x=0 |
| D、x2+y2-2x=0 |
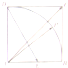如图，正方形ABCD中，E为AB上一点，P为以点A为圆心，以AB为半径的圆弧上一点，若