题目内容
18.已知△ABC的面积为S,且$\overrightarrow{BA}•\overrightarrow{CA}=S$.(1)求tanA的值;
(2)若B=$\frac{π}{4},c=6$,求△ABC的面积S.
分析 (1)设出三角形的边长,利用三角形的面积以及向量的数量积,转化求解A的正切函数值.
(2)利用两角和与差的三角函数转化求解三角形的面积即可.
解答 解:(1)由$\overrightarrow{BA}•\overrightarrow{CA}=S$,设三角形的边长为:a,b,c,则:bccosA═$\frac{1}{2}$bcsinA,
可得tanA=2.
(2)由(1)可知A∈(0,$\frac{π}{2}$),则sinA=$\frac{2\sqrt{5}}{5}$,cosA=$\frac{\sqrt{5}}{5}$,B=$\frac{π}{4},c=6$,
可得cosC=sin(A+B)=sinAcosB+cosAsinB═$\frac{2\sqrt{5}}{5}×\frac{\sqrt{2}}{2}+\frac{\sqrt{5}}{5}×\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{10}}{10}$,…(10分)
b=$\frac{csinB}{sinC}$=$\frac{6×\frac{\sqrt{2}}{2}}{\sqrt{1-(\frac{3\sqrt{10}}{10})^{2}}}$=2$\sqrt{5}$.
故S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×2\sqrt{5}×6×\frac{2\sqrt{5}}{5}$=12.…(12分)
点评 本题考查向量的数量积以及正弦定理,两角和与差的三角函数,考查转化思想以及计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织28尺,第二日,第五日,第八日所织之和为15尺,则第九日所织尺数为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
13.如图,小方格是边长为1的正方形,一个几何体的三视图如图,则几何体的表面积为( )
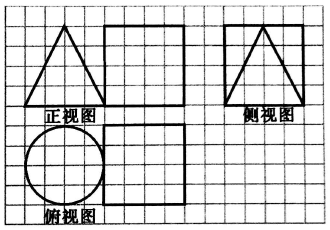

| A. | 4$\sqrt{5}π+96$ | B. | (2$\sqrt{5}+6$)π+96 | C. | (4$\sqrt{5}+4$)π+64 | D. | (4$\sqrt{5}$+4)π+96 |
3.已知偶函数y=f(x)对于任意的x∈[0,$\frac{π}{2}$)满足f′(x)cosx+f(x)sinx>0,(其中f′(x)是函数f(x)的导函数),则下列不等式中成立的是( )
| A. | $\sqrt{2}$f(-$\frac{π}{3}$)<f($\frac{π}{4}$) | B. | $\sqrt{2}$f(-$\frac{π}{3}$)<f(-$\frac{π}{4}$) | C. | f(0)$>\sqrt{2}$f(-$\frac{π}{4}$) | D. | f($\frac{π}{4}$)$<\sqrt{3}$f($\frac{π}{3}$) |
10.设{an}是首项为a1,公比为q的等比数列,则“a1q>0”是“{an}为递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |