题目内容
13．如图，小方格是边长为1的正方形，一个几何体的三视图如图，则几何体的表面积为（ ）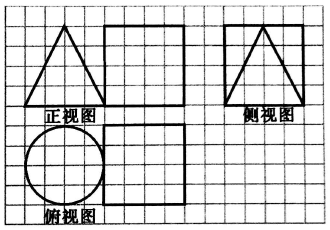
| A． | 4$\sqrt{5}π+96$ | B． | （2$\sqrt{5}+6$）π+96 | C． | （4$\sqrt{5}+4$）π+64 | D． | （4$\sqrt{5}$+4）π+96 |
分析 得到原几何体是底面半径是2、高为4的圆锥和棱长是4的正方体，即可得出结论．
解答 解：原几何体是底面半径是2、高为4的圆锥和棱长是4的正方体，
故几何体的体积是：π•22+$π•2•2\sqrt{5}$+6•42=4（$\sqrt{5}$+4）π+96，
故选：D．
点评 本题考查了三视图问题，考查面积公式，是一道基础题．
练习册系列答案
相关题目
4．已知数列{an}中a1=1，an=$\frac{1}{2}$an-1+1（n≥2），则an=（ ）
| A． | 2-（$\frac{1}{2}$）n-1 | B． | （$\frac{1}{2}$）n-1-2 | C． | 2-2n-1 | D． | 2n-1 |
8．若向量数量积$\overrightarrow{a}$•$\overrightarrow{b}$＜0则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ的取值范围是（ ）
| A． | （0，$\frac{π}{2}$） | B． | [0，$\frac{π}{2}$） | C． | （$\frac{π}{2}$，π] | D． | （$\frac{π}{2}$，π） |
如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图，则该几何体的体积为$\frac{2π}{3}$+4．