题目内容
12. 已知函数f(x)是定义在R上的奇函数,已知x≥0时,f(x)=x(2-x).
已知函数f(x)是定义在R上的奇函数,已知x≥0时,f(x)=x(2-x).(1)求函数f(x)的解析式.
(2)画出奇函数f(x)的图象.
分析 (1)当x<0时,-x>0,故f(-x)=-x(2+x),从而利用奇函数得f(x)=x(2+x),从而写出解析式;
(2)分段作出函数的图象即可.
解答 解:(1)当x<0时,-x>0,
则f(-x)=-x(2+x),
∵函数是奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)=x(2+x)
∴函数f(x)的解析式为$f(x)=\left\{\begin{array}{l}x(2-x),(x≥0)\\ x(2+x),(x<0)\end{array}\right.$;
(2)作其图象如下, .
.
点评 本题考查了函数的奇偶性的应用及学生的作图能力,注意分段作出函数的图象.

练习册系列答案
相关题目
20.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y2+y1的图象与x轴仅有一个交点,则( )
| A. | a(x2-x1)=d | B. | a(x1-x2)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
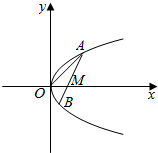 如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.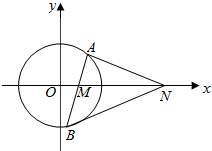 已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方