题目内容
9.△ABC的外接圆圆心为O,半径为2,$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow 0$,则$\overrightarrow{CB}$在$\overrightarrow{CA}$方向上的投影为3.分析 以O为原点建立平面直角坐标系,设A(2,0),根据条件作出图形,找到B,C的位置,求出BC,AC的长度及夹角.
解答 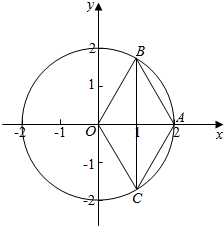 解:以O为原点建立平面直角坐标系,设A(2,0),
解:以O为原点建立平面直角坐标系,设A(2,0),
∵$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow 0$,∴AO是以AB,AC为邻边的平行四边形的对角线,
∵OB=OC,∴四边形ABOC是菱形,△AOC是等边三角形,∴B(1,$\sqrt{3}$),C(1,-$\sqrt{3}$).
∴BC=2$\sqrt{3}$,∠BCA=$\frac{1}{2}∠$ACO=30°.∴BC×cos∠BCA=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.
故答案为:3.
点评 本题考查了平面向量在几何中的应用,根据条件作出恰当的图形是关键.

练习册系列答案
相关题目
20.设二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1,0),若函数y=y2+y1的图象与x轴仅有一个交点,则( )
| A. | a(x2-x1)=d | B. | a(x1-x2)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
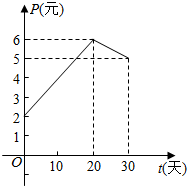 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).